
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Производная постоянной величины⇐ ПредыдущаяСтр 12 из 12
Следствие! Производная произведения функции и константы равна произведению константы на производную функции, поскольку производная константы равна нулю
1. Пусть 2. 3. Запишем очевидное отношение и найдем его предел Следствия! 1. 2. Производная степенной функции
Пусть 1. Аргументу 2. Найдем соответствующее приращение функции 3. Найдем предел
 . (1) . (1)
Производная степенной функции равна произведению показателя функции на функцию с показателем, уменьшенным на единицу, и на производную основания функции. Следствия! 1. 3. Производная показательной функции
Пусть 1. Аргументу  2. Найдем соответствующее приращение функции 3. Запишем отношение и найдем его предел
Производная показательной функции равна произведению самой функции на натуральный логарифм основания и на производную показателя. Следствия! 1. 4. Производная логарифмической функции Пусть 1. Аргументу
 . .
3. Найдем предел
Производная логарифма функции равна произведению отношению производной функции к произведению функции на натуральный логарифм основания. Следствия! 1. 5. Производные тригонометрических функций 5.1. Производная sin x Пусть 1. Аргументу 2. Найдем соответствующее приращение функции 3. Найдем предел
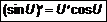 . (4) . (4)
Производная синуса функции равна произведению косинуса функции на производную функции. Следствие! 5.2. Производная cos x Пусть
Производная косинуса функции равна произведению синуса функции на производную функции с противоположным знаком. Следствие!
5.3. Производная tg x и ctg x Пусть
Производная тангенса функции равна произведению квадрата секанса функции на производную функции. Аналогично получим производную для котангенса.
Производная котангенса функции равна произведению квадрата косеканса функции на производную функции с противоположным знаком. Следствия! 1.
Пусть
Производная секанса функции равна произведению секанса функции на тангенс функции и на производную функции. Аналогично
Производная косеканса функции равна произведению косеканса функции на котангенс функции и на производную функции с противоположным знаком. Следствия! 1. 6. Производные обратных тригонометрических функций 6.1. Производная arcsin x и arccos x Пусть
Следствия! 1. 6.2. Производная arctg x и arcctg x Пусть
 дифференцируема, то дифференцируема, то
Следствия! 1. 7. Производные гиперболических функций Производная sh x, ch x, th x, cth x 1. 2. 3. 4. Если
Заключение Рассмотренные вопросы имеют больше практическое, чем теоретическое значение. Новые теории не изучались и не доказывались теоремы. Все производные получены на основе общего правила дифференцирования. Однако полученные результаты входят в основную часть таблицы производных, которую необходимо знать. Отметим, что: - производная константы равна нулю; - производная аргумента равна единице; - производная экспоненциальной функции Литература 1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – Ростов-на-Дону: Феникс, 1997. – 190 с. 2. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с.
Цель лекции: изучить понятие дифференциала; понять его геометрический смысл; научиться применять дифференциал в приближенных вычислениях. План лекции 1. Понятие дифференциала и его геометрический смысл 2. Дифференциал сложной функции 3. Дифференциалы высших порядков 4. Применение дифференциалов к приближенным вычислениям 5. Векторная функция скалярного аргумента и ее дифференциал 6. Дифференциал длины дуги Введение Ранее производные функций рассматривались как мгновенная скорость роста, то есть узнавали, во сколько раз быстрее растет функция по отношению к росту аргумента в точке. Дифференциал функции, хотя и имеет общие правила с производной в их нахождении, однако несет совершенно другой геометрический смысл, а именно: происходит не приращение функции, а приращение касательной. Это свойство используется в приближенных вычислениях, поскольку вычислить текущее значение функции прямой линии проще, чем исходной функции. Отдельно рассматривается понятие векторной функции. В силу ограниченности объема курса это понятие дается в рамках одного вопроса. Однако его понимание и дифференциала векторной функции необходимо при изучении тем: «Векторный анализ», «Интегральное исчисление» и др. Подобные функции встречаются практически во всех прикладных задачах на траекторию движения. Отдельно отметим важность понятий дифференциала функции в теме «Дифференциальные уравнения». 1. Понятие дифференциала и его геометрический смысл 1.1. Дифференциал функции ПРИМЕР 1. Для Решение.
Пусть
 следует, что следует, что  . Сравним первое слагаемое с . Сравним первое слагаемое с 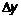 : :  . Следовательно . Следовательно  ~ ~ 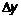 . Сравним второе слагаемое с . Сравним второе слагаемое с 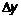 : : 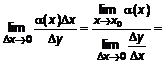 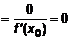 . Второе слагаемое (1) стремится к нулю быстрее, чем . Второе слагаемое (1) стремится к нулю быстрее, чем 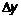 и даже и даже  . Обозначают . Обозначают  . .
Определение 1. Главная, или линейная относительно По определению
Согласно определению 1 и выражению (2) дифференциал функции определяется как
т. е. произведение производной этой функции на дифференциал независимой переменной. Из этого следует, что все формулы производных можно перенести на дифференциал. 1.2. Геометрический смысл дифференциала Пусть
 Другими словами, дифференциал функции в точке, с геометрической точки зрения, есть приращение функции касательной в точке, тогда как приращение функции есть приращение ординаты точки графика. На рис. 1 видно, что Другими словами, дифференциал функции в точке, с геометрической точки зрения, есть приращение функции касательной в точке, тогда как приращение функции есть приращение ординаты точки графика. На рис. 1 видно, что  . Очевидно, что для функции . Очевидно, что для функции  приращение касательной равно приращению функции в точке приращение касательной равно приращению функции в точке  , поскольку касательная у функции совпадает с самой функцией. , поскольку касательная у функции совпадает с самой функцией.
ПРИМЕР 2. Найти 2. Дифференциал сложной функции Если
Однако в первом случае ПРИМЕР 3. Дифференциалы Производные 3. Дифференциалы высших порядков
Дифференциал от дифференциала первого порядка называется дифференциалом второго порядка Определение 3. Дифференциал от дифференциала второго порядка называется дифференциалом третьего порядка Определение 4. Дифференциал от дифференциала Определим дифференциал второго порядка сложной функции. Если 4. Применение дифференциалов к приближенным вычислениям
 – дифференцируема в точке – дифференцируема в точке  , запишем , запишем  + + 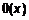 , где , где 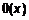 – более высокого порядка малости, чем – более высокого порядка малости, чем  . При приближенных вычислениях приращение функции можно заменить ее дифференциалом . При приближенных вычислениях приращение функции можно заменить ее дифференциалом
т. е.
Погрешность вычисления определяется выражением
ПРИМЕР 4 Найти Определим погрешность вычислений. 5. Векторная функция скалярного аргумента и ее дифференциал 5.1. Векторная функция, ее непрерывность и производная Запишем вектор
Определение 5.
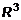 , которое каждому элементу из множества , которое каждому элементу из множества  ставит в соответствие единственный элемент из множества ставит в соответствие единственный элемент из множества 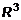 , называется векторной функцией скалярного аргумента или вектор-функцией , называется векторной функцией скалярного аргумента или вектор-функцией
Очевидно, что с изменением переменной t конец вектор-функции описывает некоторую линию в пространстве. Определение 6.
На векторную функцию переносятся все правила пределов, свойства непрерывности функции и правила дифференцирования. Определение 7. Постоянный вектор Определение 8. Векторная функция Определение 9. Производной векторной функции называется предел отношения приращения векторной функции к приращению аргумента, когда приращение аргумента стремиться к нулю 5.2. Геометрический смысл производной векторной функции Пусть векторной функции
 , т. е. , т. е.  или или  – касательный вектор. С геометрической точки зрения производная векторной функции есть вектор, касательный к годографу в данной точке. – касательный вектор. С геометрической точки зрения производная векторной функции есть вектор, касательный к годографу в данной точке.
Доказательство. 1. Дадим параметру 2. Запишем соответствующее приращение векторной функции 3. Тогда предел Следствие!
5.3. Дифференциал длины дуги
Теорема 2.
Дифференциал 5.5. Дифференциал длины дуги в различных видах I. Кривая задана параметрически
II. Функционально
III. В полярной системе
Заключение Отметим, что: - дифференциал функции это приращение касательной в точке; - дифференциал аргумента равен приращению аргумента; - дифференциал используется в приближенных вычислениях; - векторная функция это вектор с функциями координат; - производная векторной функции это касательная к годографу векторной функции; Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980. – 384 с. 2. Фихтенгольц Г.М. «Основы математического анализа» Часть 1 – М.: Лань, 2002. - 448 с.
Цель лекции: изучить основные теоремы дифференцирования; научиться использовать их для решения прикладных задач. План лекции 1. Теорема Ферма 2. Теорема Ролля 3. Теорема Лагранжа 4. Теорема Коши 5. Теорема Лопиталя 6. Общая таблица взятия пределов Введение Ранее мы изучили понятия производной и дифференциала, и научились использовать их для решения прикладных задач. Однако решение многих задач можно упростить и найти решение некоторых неразрешенных задач на основе тех теорем, которые мы изучим сегодня. Они особенно важны для решения практических задач. Для усвоения теорем необходимы знания, полученные по темам «Дифференцирование» и «Пределы». 1. Теорема Ферма 1.1. Теорема ферма Теорема 1 (Ферма). Если функция непрерывна в окрестности точки Доказательство. Пусть а) Если б) Если По условию существует производная функции, тогда односторонние пределы равны между собой. Следовательно,
Следствия! 1) Точка 2) Если не существует производной, то нет касательной. 3) Если производная 2. Теорема Роля Теорема 2 (Роля). Если функция
Доказательство. Так как 1. Хотя бы одно наибольшее или наименьшее значение функция принимает внутри отрезка
Следствие! Пусть 3. Теорема Лагранжа 3.1. Теорема
Если функция непрерывна на отрезке
Доказательство. Запишем функцию
1. Функция 2. В силу первого 3. 4. Выражение (2) удовлетворяет условиям теоремы Роля, следовательно, существует точка
6. Частный случай! Если 3.2. Геометрический смысл теоремы Очевидно (рис. 3), что тангенс угла между прямой 3.3. Формула конечных приращений Из (2) следует, что
 на приращение аргумента. Эта формула используется для оценки погрешностей приближенных вычислений функции с помощью дифференциала. Из (3) точное значение дифференцируемой функции определяется как на приращение аргумента. Эта формула используется для оценки погрешностей приближенных вычислений функции с помощью дифференциала. Из (3) точное значение дифференцируемой функции определяется как
а приближенное значение как
Тогда погрешность будет определяться разностью между точным и приближенным значением
4. Теорема Коши Теорема 4 (Коши). Если функции
 . (5) . (5)
Доказательство аналогично теореме Лагранжа. При этом записывают функцию
Частный случай! |
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 612. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Производная постоянной величины (рис. 1), т. е. функции
Производная постоянной величины (рис. 1), т. е. функции  , была рассмотрена в примере 1 (см. л. 6, ч. 2). Напомним, что приращение функции
, была рассмотрена в примере 1 (см. л. 6, ч. 2). Напомним, что приращение функции 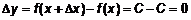 , следовательно,
, следовательно,  , т. е.
, т. е. 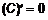 . Другими словами, угол между прямой
. Другими словами, угол между прямой  и осью
и осью 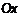 равен
равен  , т. е. прямая
, т. е. прямая  .
. дадим приращение
дадим приращение  Найдем соответствующее приращение функции
Найдем соответствующее приращение функции 
 .
. , то есть
, то есть  (см. рис. 2).
(см. рис. 2).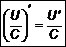 2.
2.  3.
3. 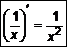
 , где
, где  ,
,  дадим приращение
дадим приращение  – приращение
– приращение  , и новое значение
, и новое значение  .
. =
=  .
. . Из необходимого условия дифференцируемости следует, что бесконечно малому приращению аргумента
. Из необходимого условия дифференцируемости следует, что бесконечно малому приращению аргумента  , то есть получаем неопределенность
, то есть получаем неопределенность  . Тогда последний предел
. Тогда последний предел 

 =
=  , откуда согласно пятому замечательному пределу имеем
, откуда согласно пятому замечательному пределу имеем  . 2.
. 2.  . 3.
. 3.  .
. , где
, где  ,
,  .
.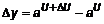 .
. =
=  . Из необходимого условия дифференцируемости следует, что бесконечно малому приращению аргумента
. Из необходимого условия дифференцируемости следует, что бесконечно малому приращению аргумента  = =
= =  =
=  , откуда согласно четвертому замечательному пределу имеем
, откуда согласно четвертому замечательному пределу имеем  . (2)
. (2) . 2.
. 2.  .
. , где
, где  .
.
 =
= 
 . Из необходимого условия дифференцируемости следует, что бесконечно малому приращению аргумента
. Из необходимого условия дифференцируемости следует, что бесконечно малому приращению аргумента 
 , откуда согласно третьему замечательному пределу имеем
, откуда согласно третьему замечательному пределу имеем  , или
, или . (3)
. (3) . 2.
. 2.  . 3.
. 3. 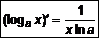 .
.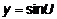 , где
, где 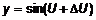 .
. .
. =
=  =
=  , или
, или .
.  , где
, где 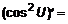
 . С другой стороны,
. С другой стороны, 



 . Откуда
. Откуда . (5)
. (5) .
. , где
, где 

 . (6)
. (6) . (7)
. (7) . 2.
. 2. 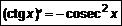 .
. , где
, где  , или
, или . (8)
. (8) . (9)
. (9) . 2.
. 2.  .
. , где
, где  ,
,  . Воспользуемся теоремой о производной обратной функции
. Воспользуемся теоремой о производной обратной функции  . Запишем
. Запишем  . Тогда
. Тогда 



 . Если
. Если  . Аналогично
. Аналогично  . (10)
. (10)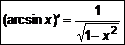 . 2.
. 2.  .
. , где
, где 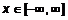 ,
,  . Тогда
. Тогда 


 .
. . Аналогично
. Аналогично  . (11)
. (11) . 2.
. 2.  .
. ,
,  .
.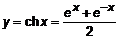 ,
,  .
. , тогда
, тогда 
 .
. , тогда
, тогда 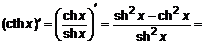
 .
.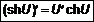 ,
,  ,
,  ,
,  .
. равна самой функции.
равна самой функции. при приращении
при приращении 
 Таким образом,
Таким образом,  или
или  , следовательно, по второму определению предела
, следовательно, по второму определению предела  – бесконечно малая величина в точке
– бесконечно малая величина в точке  , (1)
, (1) .
. . Для любых
. Для любых  . Если
. Если  , то
, то  =
=  , или
, или . (2)
. (2) , (3)
, (3) некоторую точку на кривой (рис. 1), приращение
некоторую точку на кривой (рис. 1), приращение  . В
. В 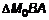 обозначим угол
обозначим угол  . Определим
. Определим  =
= 
 , или
, или  .
. для
для  . Имеем
. Имеем  .
.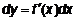 . Если
. Если  – дифференцируемые функции,
– дифференцируемые функции,  – независимая переменная, тогда
– независимая переменная, тогда  – сложная функция,
– сложная функция,  . Сравнивая оба дифференциала простой и сложной функций, замечаем, что форма дифференциала не изменилась, то есть она не зависит от того, является ли аргумент независимой переменной или функцией. Это свойство называется инвариантностью дифференциала
. Сравнивая оба дифференциала простой и сложной функций, замечаем, что форма дифференциала не изменилась, то есть она не зависит от того, является ли аргумент независимой переменной или функцией. Это свойство называется инвариантностью дифференциала . (4)
. (4) – число, а во втором случае
– число, а во втором случае  – функция.
– функция.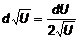 ,
,  – инвариантны.
– инвариантны. ,
,  – не инвариантны.
– не инвариантны. . Поскольку
. Поскольку 
 . (5)
. (5) =
= 
 . (6)
. (6) порядка называется дифференциалом n-го порядка
порядка называется дифференциалом n-го порядка  = =
= = 
 . (7)
. (7) . Если
. Если  . Однако
. Однако 
 . Сравнивая оба дифференциала простой и сложной функций, замечаем, что дифференциал второго, следовательно, и дифференциалы больших порядков не инвариантны.
. Сравнивая оба дифференциала простой и сложной функций, замечаем, что дифференциал второго, следовательно, и дифференциалы больших порядков не инвариантны. , (8)
, (8) , тогда
, тогда  , откуда
, откуда . (9)
. (9) , где
, где 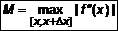 . (10)
. (10)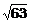 . Запишем соответствующую функцию
. Запишем соответствующую функцию  , точку
, точку  , приращение
, приращение  , значение функции в точке
, значение функции в точке  , производную
, производную  и значение производной в точке
и значение производной в точке  . Тогда, используя выражение (9), определим
. Тогда, используя выражение (9), определим  .
. . Данная функция убывает на отрезке
. Данная функция убывает на отрезке  , следовательно,
, следовательно,  . Тогда
. Тогда  . С учетом погрешности
. С учетом погрешности  .
. . Если
. Если  , то вектор
, то вектор  – постоянный, если
– постоянный, если  ,
, 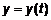 и
и  – функции, то
– функции, то  . (11)
. (11) .
. Линия, описываемая концом векторной функции, называется годографом
Линия, описываемая концом векторной функции, называется годографом  векторной функции. Начало векторной функции называется полюсом (рис. 2).
векторной функции. Начало векторной функции называется полюсом (рис. 2).  называется пределом векторной функции
называется пределом векторной функции  в
в  , если для любых
, если для любых 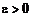 существует
существует  , такая, что для любых
, такая, что для любых  следует
следует  , или по второму определению предела
, или по второму определению предела  есть бесконечно малая величина в точке
есть бесконечно малая величина в точке 
 . (12)
. (12) соответствует приращение на
соответствует приращение на  (рис. 3). Очевидно, что вектор
(рис. 3). Очевидно, что вектор  . При
. При 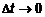 точка
точка  на кривой L
на кривой L  Теорема 1.
Теорема 1. . (13)
. (13)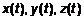 также получать соответствующие приращения
также получать соответствующие приращения  .
. .
. , откуда
, откуда  .
.  (14)
(14) Пусть L – годограф непрерывной векторной функции
Пусть L – годограф непрерывной векторной функции  на кривой L (рис. 4). Очевидно, что длина дуги будет некоторой функцией
на кривой L (рис. 4). Очевидно, что длина дуги будет некоторой функцией  .
. (15)
(15) . Но
. Но 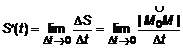 . Очевидно, что при
. Очевидно, что при  справедливо
справедливо  , тогда
, тогда 
 , откуда справедливо (15).
, откуда справедливо (15). . По теореме Пифагора
. По теореме Пифагора  , или
, или . (16)
. (16) , или
, или . (17)
. (17) ,
, 
 , или
, или . (18)
. (18) – наибольшее значение функции
– наибольшее значение функции 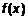 , следовательно,
, следовательно,  для всех
для всех  или
или 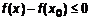 . Тогда
. Тогда 
 . Возможны два варианта.
. Возможны два варианта. , т. е.
, т. е.  , и
, и  ,
, , т. е.
, т. е.  , и
, и  .
. =
=  =0, или
=0, или  . Аналогично доказывается случай
. Аналогично доказывается случай  1.2. Геометрический смысл теоремы Ферма
1.2. Геометрический смысл теоремы Ферма , то касательная вертикальна.
, то касательная вертикальна. , то хотя бы в одной точке внутри отрезка производная этой функции равна нулю
, то хотя бы в одной точке внутри отрезка производная этой функции равна нулю .
. , то по теореме Вейерштрасса эта функция принимает на этом отрезке наибольшее и наименьшее значения. Возможны два случая.
, то по теореме Вейерштрасса эта функция принимает на этом отрезке наибольшее и наименьшее значения. Возможны два случая. , т. е. в этой точке выполняются условия теоремы Ферма и
, т. е. в этой точке выполняются условия теоремы Ферма и  .
. 2. Наибольшее и наименьшее значение функция принимает на концах отрезка
2. Наибольшее и наименьшее значение функция принимает на концах отрезка  – наименьшее значение,
– наименьшее значение,  – наибольшее значение. Тогда по теореме Больцано–Коши
– наибольшее значение. Тогда по теореме Больцано–Коши  . Однако по условию т.
. Однако по условию т.  , следовательно,
, следовательно, 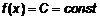 и
и  , тогда между двумя нулями функции находится хотя бы один нуль производной (рис. 2).
, тогда между двумя нулями функции находится хотя бы один нуль производной (рис. 2).
 . (1)
. (1) . (2)
. (2)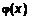 – непрерывна на
– непрерывна на  .
.
 .
.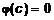 .
. 5. Найдем
5. Найдем 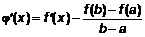 .
. . Из п. 4 следует, что
. Из п. 4 следует, что  при
при  . Геометрическая интерпретация теоремы представлена на рис. 3.
. Геометрическая интерпретация теоремы представлена на рис. 3.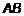 и осью
и осью  . С другой стороны,
. С другой стороны,  . Если функция
. Если функция  найдется такая точка
найдется такая точка  , касательная в которой к этой функции параллельна хорде, стягивающей концы кривой.
, касательная в которой к этой функции параллельна хорде, стягивающей концы кривой. . Если
. Если  , а
, а 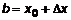 , то
, то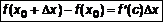 . (3)
. (3) ,
, .
. –
– 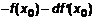


 . Применим теорему Лагранжа
. Применим теорему Лагранжа 
 . Очевидно (рис. 3), что
. Очевидно (рис. 3), что  . Обозначим
. Обозначим  , тогда максимальную погрешность можно оценить как
, тогда максимальную погрешность можно оценить как . (4)
. (4) непрерывны на отрезке
непрерывны на отрезке  для любых
для любых  , то существует точка
, то существует точка  .
.