
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Непрерывность функции в точке и на интервалеТочки разрыва функции, их классификация 3. Основные теоремы о непрерывных функциях 4. Свойства функций, непрерывных на отрезке 5. Метод половинного деления Введение Данная лекция базируется на знаниях, полученных на предыдущих лекциях, и позволяет перейти к важной теме «Дифференциальное исчисление». Для изучения понятия производной необходимо понимать непрерывность функции. Несмотря на очевидность многих теорем, требуется уделить им особое внимание, так как незначительное отклонение от накладываемых на функцию условий приводит к существенным ошибкам. Например, важна непрерывность функции не на интервале, а на отрезке или различие между понятиями максимума функции и наибольшего значения функции на отрезке и т.д. Отдельно рассмотрим метод половинного деления. Он основан на знании прежде всего теорем о непрерывных функциях и уже относится к численным методам. Непрерывность функции в точке и на интервале Непрерывность функции Пусть функция Определение 1. Функция Равенство (1) означает выполнение трех условий: 1) функция 2) функция 3) предел функции в точке Замечание!
 , то равенство (1) можно записать в виде , то равенство (1) можно записать в виде   . Это означает, что при нахождении предела непрерывной функции можно перейти к пределу под знаком функции, т. е. в функцию . Это означает, что при нахождении предела непрерывной функции можно перейти к пределу под знаком функции, т. е. в функцию 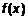 вместо аргумента вместо аргумента  подставить его предельное значение подставить его предельное значение  . . ПРИМЕР 1. В силу непрерывности функции 1.2. Приращение аргумента и функции
Пусть функция Согласно определению Выражение (2) является еще одним определением непрерывности функции в точке. Определение 3.
 называется непрерывной в точке называется непрерывной в точке  и ее окрестности, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. и ее окрестности, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
ПРИМЕР 2. Исследуем на непрерывность функцию Определение 4. Функция Определение 5. Функция 2. Точки разрыва функции, их классификация Определение 6. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции, то есть точками, в которых не выполняется хотя бы одно из условий (1). 1) Функция определена в окрестности точки 2) Функция определена в точке
 и ее окрестности, существует предел и ее окрестности, существует предел  , но этот предел не равен значению функции в точке , но этот предел не равен значению функции в точке  (рис. 4). (рис. 4).
Определение 7. Точка разрыва Определение 8. Точка разрыва Соответственно на рис. 2 точка 3. Основные теоремы о непрерывных функциях Теоремы о непрерывности функций следуют из соответствующих теорем о пределах. Теорема 1. Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного, за исключением тех значений аргумента, в которых делитель равен нулю). Доказательство. Пусть функции
 , ,
т. е. Теорема 2. Если функция Доказательство. В силу непрерывности функции
Следовательно, функция Теорема 3. Если функция Важно! Все элементарные функции непрерывны в области определения. ПРИМЕР 3.
4. Свойства функций непрерывных на отрезке Непрерывные на отрезке функции имеют ряд важных свойств. Теорема 4 (Вейерштрасса). Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений. Изображенная на рис. 5 функция Теорема 5.
 Если функция непрерывна на отрезке, то она ограничена на этом отрезке (вытекает из теоремы 4). Если функция непрерывна на отрезке, то она ограничена на этом отрезке (вытекает из теоремы 4).
Теорема 6 (Больцано-Коши). Если функция Геометрически теорема очевидна (рис. 6). Для любого числа С, заключенного между А и В, внутри этого отрезка найдется такая точка с, что Теорема 7. Если функция Геометрический смысл теоремы (рис. 7) означает, что если график непрерывной функции переходит с одной стороны оси Следствие! Теорема 7 лежит в основе так называемого метода половинного деления, который используется для нахождения корня уравнения ПРИМЕР 4. Определить с точностью
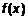 . .
Шаг 1. Шаг 2. Вычисляем Шаг 3. Вычисляем Шаг 4. При Шаг 5. Если Заключение Для анализа функции необходимы знания о пределах. Последний пример – численный метод анализа функции. Отметим: - функция непрерывна, если выполняются три условия; - из непрерывности функции - приращение функции в точке - точки разрыва бывают первого и второго рода; - метод половинного деления позволяет найти корень уравнения с заданной точностью; - Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980. – 384 с. 2. Натансон И.П. «Теория функций вещественной переменной». – СПб.: Лань, 1999. - 560 с.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 631. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . (1)
. (1) ;
; справедливо
справедливо  .
. Определение 2.
Определение 2. . Возьмем произвольную точку
. Возьмем произвольную точку  . Для любого
. Для любого  разность
разность  называется приращением аргумента
называется приращением аргумента  в точке
в точке  . Разность соответствующих значений функций
. Разность соответствующих значений функций  называется приращением функции
называется приращением функции  ,
,  (рис.1). Очевидно, что эти приращения могут быть как положительными, так и отрицательными числами. Так как
(рис.1). Очевидно, что эти приращения могут быть как положительными, так и отрицательными числами. Так как  , то равенство (1) можно записать
, то равенство (1) можно записать  , или
, или . (2)
. (2) . Определим
. Определим  , или
, или  =
=  . Согласно (2)
. Согласно (2)  , то есть функция
, то есть функция  .
. , если она непрерывна в интервале
, если она непрерывна в интервале  непрерывна справа
непрерывна справа  , а в точке
, а в точке  непрерывна слева
непрерывна слева  .
.
 ,
,  и при этом, если
и при этом, если  , то точка
, то точка  , точка
, точка 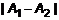 называется скачком функции в точке разрыва первого рада.
называется скачком функции в точке разрыва первого рада. и
и  . На рис. 3. точка
. На рис. 3. точка 

 . Скачок функции в точке
. Скачок функции в точке 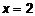 соответственно равен
соответственно равен 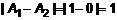 . На рис. 4. точка
. На рис. 4. точка 
 . Если установить, что
. Если установить, что  при
при  непрерывны на некотором множестве X и
непрерывны на некотором множестве X и  . Применяя теорему о пределе произведения, получим
. Применяя теорему о пределе произведения, получим . Следовательно,
. Следовательно, 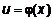 непрерывна в точке
непрерывна в точке  непрерывна в точке
непрерывна в точке  , то сложная функция
, то сложная функция  , состоящая из непрерывных функций, непрерывна в точке
, состоящая из непрерывных функций, непрерывна в точке  , т. е. при
, т. е. при  . Поэтому в силу непрерывности функции
. Поэтому в силу непрерывности функции  .
.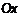 , то обратная функция
, то обратная функция  также непрерывна и монотонна на соответствующем отрезке
также непрерывна и монотонна на соответствующем отрезке 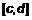 оси
оси  .
. непрерывна , тогда
непрерывна , тогда  .
. непрерывна на отрезке
непрерывна на отрезке  . Для любого
. Для любого  имеет место неравенство
имеет место неравенство  .
.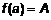 и
и  , то на этом отрезке она принимает и все промежуточные значения между А и В.
, то на этом отрезке она принимает и все промежуточные значения между А и В. . Прямая
. Прямая  пересечет график функции по крайней мере в одной точке, иначе функция должна была бы иметь разрыв.
пересечет график функции по крайней мере в одной точке, иначе функция должна была бы иметь разрыв. .
. .
.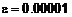 корень для
корень для  на отрезке
на отрезке  , применив метод половинного деления.
, применив метод половинного деления. = - 2.281718 и
= - 2.281718 и  =16.085537.
=16.085537. .
. =3.096163. Если
=3.096163. Если  , если
, если  , то полагаем
, то полагаем 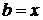 ,
,  , иначе
, иначе  ,
,  . В нашем случае
. В нашем случае  , поэтому
, поэтому 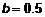 ,
,  =3.096163.
=3.096163.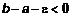 , то задача решена. В качестве искомого корня (с заданной точностью
, то задача решена. В качестве искомого корня (с заданной точностью  ) принимают
) принимают  . Иначе процесс деления отрезка
. Иначе процесс деления отрезка  , следовательно, возвращаемся к шагу 2,
, следовательно, возвращаемся к шагу 2,  , а новое значение
, а новое значение  =–0.018311. Поскольку
=–0.018311. Поскольку  , то
, то  , а
, а 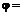 -0.018311. Определяем
-0.018311. Определяем  . И так далее. В конечном счете получим x = 0.29589.
. И так далее. В конечном счете получим x = 0.29589.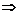 , что
, что  соответствует
соответствует  ;
; ;
; ,
, 

 . Откуда
. Откуда  . Напомним, что
. Напомним, что  ~
~