
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные теоремы о пределахТеорема 1. Предел постоянной величины Теорема 2. Предел алгебраической суммы конечного числа функций, имеющих предел в точке, равен алгебраической сумме пределов этих функций
Теорема 3. Предел произведения конечного числа функций, имеющих предел в точке, равен произведению пределов этих функций
Теорема 4.
Доказательство (основано на втором определении пределов). Пусть
Обозначим Следствия! 1) ПРИМЕР 1.
Если функция определена в точке, то для вычисления предела достаточно в эту функцию подставить предельное значение.
Теорема 5. Если функции
Пусть 3. Первый замечательный предел Докажем справедливость рассмотренного в лекции 2 предела
Согласно рис. 2. имеет место соотношение площадей 
Используя этот предел можно доказать другие пределы 1) 2) 3) Таким образом, при нахождении пределов можно делать эквивалентные замены бесконечно малых величин 1) 4) 4. Числовая последовательность и ее предел, второй замечательный предел 4.1. Определения Определение 1. Числовой последовательностью называется функция натурального аргумента: Определение 2. Число b называется пределом числовой последовательности, если Определение 3. Числовая последовательность, имеющая предел, называется сходящейся, а не имеющая называется расходящейся. 4.2. Геометрический смысл числовой последовательности
Замечание! Всякая ограниченная и монотонная функция натурального аргумента (числовая последовательность) имеет предел.
Так, например, доказано, что числовая последовательность
Выражение (5) называется вторым замечательным пределом. Второй замечательный предел служит для вычисления пределов функций, имеющих неопределенность
Очевидно, что справедливы следующие пределы
ПРИМЕР 2.
5.1. Третий замечательный предел
Доказательство.
5.2. Четвертый замечательный предел
Доказательство. Обозначим 5.3. Пятый замечательный предел
В частности
Заключение
 . Полученные начальные знания о числовых последовательностях позволят лучше теорию рядов. Отметим один из используемых способов нахождения пределов: предел логарифма равен логарифму предела. Данный способ позволяет раскрывать степенные или показательные неопределенности. Особую роль отметим в применении замен эквивалентных бесконечно малых величин. . Полученные начальные знания о числовых последовательностях позволят лучше теорию рядов. Отметим один из используемых способов нахождения пределов: предел логарифма равен логарифму предела. Данный способ позволяет раскрывать степенные или показательные неопределенности. Особую роль отметим в применении замен эквивалентных бесконечно малых величин.
В прикладных вопросах задача нахождения предела, как будет показано далее, встречается практически всегда, когда необходимо анализировать графические зависимости, будь то графики в экономике, графики зависимости популяций в биологии и др. Отметим наиболее важные аспекты: - сумма или разность бесконечно малых величин равна бесконечно малой величине меньшего порядка малости - на основе замечательных пределов можно заменять эквивалентные величины; - числовая последовательность есть функция натурального аргумента; - очевидно, что при приближенных расчетах можно вместо функции можно использовать эквивалентную ей величину - экспонента – это предел числовой последовательности.
Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980. – 384 с. 2. Фихтенгольц Г.М. «Основы математического анализа» Часть 1 – М.: Лань, 2002. - 448 с. 3. Фихтенгольц Г.М. «Основы математического анализа» Часть 2 – М.: Лань, 2002. - 464 с. 4. Натансон И.П. «Теория функций вещественной переменной». – СПб.: Лань, 1999. - 560 с. 5. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с.
Цель лекции: изучить понятие непрерывности функции в точке и на отрезке; научиться определять и классифицировать точки разрыва функции; на основе теорем и свойств непрерывных функций научиться находить корни уравнений методом половинного деления. План лекции |
||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 578. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 есть сама постоянная величина
есть сама постоянная величина . (1)
. (1) при
при  . (2)
. (2) при
при  при
при  . (3)
. (3) и
и  . Необходимо доказать, что
. Необходимо доказать, что 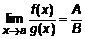 , то есть показать, что
, то есть показать, что  – бесконечно малая величина.
– бесконечно малая величина. 

 .
. и
и  – бесконечно малые величины, тогда
– бесконечно малые величины, тогда 
 – произведение бесконечно малой величины на ограниченную функцию есть бесконечно малая величина.
– произведение бесконечно малой величины на ограниченную функцию есть бесконечно малая величина. 2)
2)  .
. Вывод!
Вывод!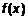 и
и  имеют в точке одинаковый предел, а в окрестности этой точки справедливы неравенства
имеют в точке одинаковый предел, а в окрестности этой точки справедливы неравенства 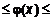
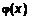 имеет тот же предел.
имеет тот же предел. Доказательство.
Доказательство. . Тогда согласно определению предела
. Тогда согласно определению предела 


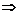
 и
и  , откуда
, откуда  и
и  . С учетом неравенств запишем
. С учетом неравенств запишем 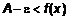
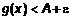 , или
, или 
 , следовательно
, следовательно  (рис. 1).
(рис. 1). . (4)
. (4)

 . Площади определяются как
. Площади определяются как  ,
, 
 ,
, 

 . Тогда
. Тогда 

 , или
, или 
 . Следовательно,
. Следовательно, 
 . Перейдем к пределам
. Перейдем к пределам 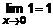 ,
,  . Согласно теореме 5 определим
. Согласно теореме 5 определим  . Выражение (4) называется первым замечательным пределом.
. Выражение (4) называется первым замечательным пределом. ;
; ;
; =
=  =
=  .
. ~
~  ; 2)
; 2) 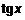 ~
~  ~
~  ;
;  ~
~  ~
~ 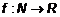 или
или  ,
, 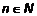 . Обозначается последовательность
. Обозначается последовательность 

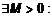
 , справедливо неравенство
, справедливо неравенство 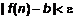 .
. Представим систему координат, в которой по оси абсцисс отложены натуральные числа, а по оси ординат – значения функции натурального аргумента. Как видно рис. 3, наличие предела числовой последовательности означает, что после некоторого значения n значения функции не будут выходить за диапазон
Представим систему координат, в которой по оси абсцисс отложены натуральные числа, а по оси ординат – значения функции натурального аргумента. Как видно рис. 3, наличие предела числовой последовательности означает, что после некоторого значения n значения функции не будут выходить за диапазон  . Причем, какое бы значение
. Причем, какое бы значение  мы ни выбрали, всегда найдется такое значение n, после которого данное неравенство будет иметь место.
мы ни выбрали, всегда найдется такое значение n, после которого данное неравенство будет иметь место. , следовательно, она ограничена сверху и имеет предел
, следовательно, она ограничена сверху и имеет предел или
или  . (5)
. (5) . Другая запись второго замечательного предела:
. Другая запись второго замечательного предела: . (6)
. (6) или
или  (7)
(7) , где
, где  .
. . (9)
. (9) . Частный случай
. Частный случай  .
. . (10)
. (10) , тогда
, тогда  . С учетом обозначений
. С учетом обозначений  . Согласно третьему замечательному пределу
. Согласно третьему замечательному пределу  . Частный случай
. Частный случай  .
. . (11)
. (11)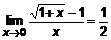 , и к уже известным нам эквивалентностям добавим
, и к уже известным нам эквивалентностям добавим
 ;
; ;
;