
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Физический и геометрический смысл производнойПусть функция - аргументу - найдем приращение функции - составим отношение приращения функции к аргументу - найдем предел этого отношения при
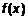 и обозначают одним символом и обозначают одним символом  . .
Определение 3. Производной функции Замечание! Производная функции Определение 4. Функция Значение производной функции ПРИМЕР 1. Найти производную функции Решение: - аргументу - приращение функции - составим отношение - найдем предел ПРИМЕР 2. Найти производную функции Решение: - аргументу - найдем соответствующее приращение функции - составим отношение - найдем Вернемся к перемещению точки. Было получено
Скорость прямолинейного движения материальной точки в момент времени t есть производная от пути по времени. В этом заключается физический смысл производной. Другими словами, производная показывает, во сколько раз быстрее возрастает значение функции по отношению к росту переменной, или какова мгновенная скорость протекания процесса, описываемого некоторой функцией.  Вернемся к задаче с касательной к кривой. Был найден угловой коэффициент касательной Замечание! То есть производная 2.2. Уравнение касательной и нормали к кривой
Определение 2. Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой. Нормаль перпендикулярна касательной, то ее угловой коэффициент
Поэтому уравнение нормали будет иметь вид (при
Теорема 1. Если
Теорема 2. Если функция дифференцируема в некоторой точке, то она непрерывна в ней. Доказательство. Пусть функция
Обратная теорема не верна. Непрерывная функция может не иметь производной. Пример: Замечание! Производная непрерывной функции Определение 3. Если функция Заключение Отметим наиболее важные моменты: - производная непрерывной функции необязательно непрерывна; - если функция дифференцируема в некоторой точке, то она непрерывна в ней; - функция, дифференцируемая в некоторой точке, не обязательно непрерывна; - тангенс угла наклона определяет уравнение касательной и нормали к кривой. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980. – 384 с. 2. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с.
Цель лекции: изучить правила дифференцирования функций; научиться применять эти правила при решении прикладных задач. План лекции |
||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 678. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 определена на некотором интервале
определена на некотором интервале  . Осуществим следующие операции:
. Осуществим следующие операции: дадим приращение
дадим приращение  :
: 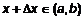 ;
; ;
; ;
; :
:  .
. называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. . (4)
. (4) , произведенная из данной функции.
, произведенная из данной функции. обозначается одним из символов
обозначается одним из символов  или
или  .
.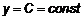 .
. дадим приращение
дадим приращение 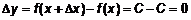 ;
; ;
; , т. е.
, т. е. 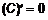 .
. .
.
 ;
; ;
; или
или 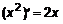 .
. .
.
 .
. в точке x равна угловому коэффициенту касательной к графику функции
в точке x равна угловому коэффициенту касательной к графику функции  Если точка касания M имеет координаты
Если точка касания M имеет координаты 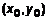 (рис. 4), то угловой коэффициент касательной есть
(рис. 4), то угловой коэффициент касательной есть  . Воспользуемся уравнением прямой, проходящей через заданную точку в заданном направлении
. Воспользуемся уравнением прямой, проходящей через заданную точку в заданном направлении . (5)
. (5) . (6)
. (6) )
)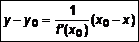 . (7)
. (7)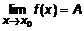 , то
, то 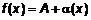 .
. . Отсюда имеем
. Отсюда имеем  , где
, где 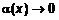 при
при  . Переходя к пределу при
. Переходя к пределу при  . Это означает, что функция
. Это означает, что функция  Замечание!
Замечание! в точке
в точке  (рис. 5).
(рис. 5).