
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение предела функции в точкеТеорема единственности предела функции в точке 3. Односторонние пределы, необходимые и достаточные условия существования предела функции в точке 4. Свойства функции, имеющей предел в точке 5. Предел функции на бесконечности Введение Дальнейшее изучение интегро-дифференциального счисления невозможно без понимания предела. Это понятие будет встречаться на протяжении не только всего курса высшей математики, но и на других смежных дисциплинах. Понимание материала как этой, так и последующих лекций лежит в большей части в интуитивной области, однако очень важно внимательно изучить первые два определения и понять их геометрический смысл, они являются базовыми в дальнейшем. Определение предела функции в точке Определение предела Определение 1. Число b называется пределом функции Или то же определение с использованием сокращений
Определение 2.
ПРИМЕР 1. Функция Важно! На величину предела не влияет поведение функции в конечном числе точек дельта окрестности. Эти точки можно исключить и взять другую, меньшую дельта-окрестность.  ПРИМЕР 2. Доказать, что Теорема единственности предела функции в точке Теорема 1. Если функция имеет предел в точке, то он единственный. Доказательство (от противного). Предположим, что
условия существования предела функции в точке Обозначим Обозначим Определение 3. Число b называется левосторонним пределом функции Определение 4. Число b называется правосторонним пределом функции Теорема 2. Для того чтобы функция имела предел, необходимо и достаточно, чтобы существовали левосторонний и правосторонний пределы и были равны между собой. Доказательство. Необходимость. Дано: Достаточность. Дано:
  . а по условию и определению 4 . а по условию и определению 4     . Примем за . Примем за  . Тогда . Тогда    (рис. 2). (рис. 2).
4. Свойства функции, имеющей предел в точке Теорема 3. Если функция имеет положительный предел в точке, то найдется окрестность точки, в которой функция положительна. Доказательство. Из определения следует, что Определение 5. Функция ПРИМЕР 3.
Теорема 4. Если функция имеет конечный предел в точке, то она ограничена в некоторой окрестности этой точки. Доказательство. Пусть Теорема 5.
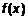 имеет конечный предел в точке, то имеет конечный предел в точке, то  ограничена в некоторой окрестности этой точки. ограничена в некоторой окрестности этой точки.
Доказательство аналогично теореме 4. 5. Предел функции на бесконечности
N–окрестностью бесконечно удаленной точки называется множество всех точек рас, стояние до которых большее N или Определение 7. Число b называется пределом функции Замечание! Так как принципиального различия между определениями 7 и 1, 2 нет, то все рассмотренные теоремы можно отнести к функциям, имеющим предел на бесконечности. Заключение В заключении важно отметить, что предел – это абстрактное понятие, записанное строгим математическим языком, т. е. предел – это то значение, к которому стремится функция, причем она его может никогда не достичь (функция в этой точке может не существовать). Отметим, что предел функции в точке можно понимать как бесконечность вселенной и времени. Отметим, что: - предел – это абстракция, к которой что-то стремиться; - функция ограничена в окрестностях, где она имеет предел; - односторонние пределы могут быть не равными, т.е. может быть разрыв; - доказательство всех теорем о пределах базируется на фундаментальном определении самого предела; - функция может быть ограничена на бесконечности; - всегда можно взять дельта-окрестность меньше той, которая дана. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980. 2. Фихтенгольц Г.М. «Основы математического анализа» Часть 1 – М.: Лань, 2002, - 448 с. 3. Натансон И.П. «Теория функций вещественной переменной». – СПб.: Лань, 1999, - 560 с. Лекция 3. Бесконечно малые и бесконечно большие величины
План лекции Бесконечно малые величины Второе определение предела 3. Свойства бесконечно малых величин 4. Бесконечно большие величины 5. Сравнение бесконечно малых величин Введение Данная лекция посвящена наиболее трудно усваиваемым понятиям: «бесконечно малая и бесконечно большая величина». Дело в том, что структура всего математического анализа построена на подобных понятиях. Ясно, что представить точку с нулевым размером или бесконечную область так же трудно, как представить бесконечную вселенную и абсолютно элементарную частицу. Данные понятия находятся больше в области абстрактного. Каждый находит собственное понимание этого вопроса, однако должны быть незыблемыми основные правила и теоремы, которым подчиняются эти величины. Следует обратить внимание на то, что величина, обратная бесконечно малой величине, есть бесконечно большая величина. Аналог в астрофизике – рождение бесконечной вселенной происходит из точки нулевого размера (большой врыв). Бесконечно малые величины Определение 1. Функция ПРИМЕР 1.
Замечание! Понятие «бесконечно малая» величина нельзя смешивать с понятием «очень малая величина», т. к. последняя является константой, а бесконечно малая величина – переменная, промежуточные значения которой могут быть и большими, но ее предел стремится к нулю. Определение 2. Определение на языке
Теорема 1. Для того чтобы b было пределом функции Доказательство. Необходимость. Дано: Достаточность. Дано: Определение 3. Второе определение предела. Число b называется пределом функции 3. Свойства бесконечно малых величин 3.1. Сумма бесконечно малых величин Теорема 2. Алгебраическая сумма конечного числа бесконечно малых величин в точке есть величина бесконечно малая в этой точке, т. е. Доказательство. Докажем, что теорема верна для двух слагаемых: Если
Если число слагаемых 3.2. Произведение бесконечно малой величины в точке на функцию Теорема 3. Произведение бесконечно малой величины в точке на функцию, ограниченную в окрестности этой точки, есть бесконечно малая величина. Доказательство. Пусть Важно! Очевидно, что произведение n бесконечно малых величин есть бесконечно малая величина. Если число произведений
Определение 3. Функция ПРИМЕР 2. Важно! Бесконечно большую величину нельзя путать с очень большой величиной (const). Среди постоянных чисел есть 0, его можно принять за бесконечно малую величину, за бесконечно большую величину ни одно из чисел принять нельзя. Теорема 4. Величина, обратная бесконечно малой величине в некоторой точке, есть величина бесконечно большая и наоборот. Доказательство. а) По условию б) Пусть Следствие! При нахождении пределов можно делать замену Вопрос 5. Сравнение бесконечно малых величин Пусть
Теорема 5. Предел отношения бесконечно малых величин в некоторой точке равен пределу отношения эквивалентных им бесконечно малых величин в этой точке. Если
 . .
Доказательство.
Следствие! В частности, если ПРИМЕР 3.
Заключение В большей части курса математики будем пользоваться множеством действительных чисел, которое обладает свойством непрерывности, плотности и упорядоченности, то есть математическим представлением восприятия окружающего пространства. Отметим, что: - бесконечно малая и бесконечно большая величины это функции; - предел бесконечно малой величины в точке равен нулю; - предел бесконечно большой величины есть бесконечность - сумма бесконечно малых величин есть бесконечно малая величина; - бесконечно большая и бесконечно малая величины связаны между собой однозначным обратно пропорциональным преобразованием; - величины бывают разного порядка малости, т. е. скорость убывания бесконечно малых функций может быть различна; - сравнение бесконечно малых величин происходит на основании определения предела их отношения; - в пределах можно переходить от бесконечно малых к бесконечно большим величинам. Литература 1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001. 2. Натансон И.П. «Теория функций вещественной переменной». – СПб.: Лань, 1999, - 560 с. |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 501. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , если для любого сколь угодно малого положительного
, если для любого сколь угодно малого положительного  найдется другое положительное число
найдется другое положительное число  , такое, что для всех x, быть может, не равных a и удовлетворяющих неравенству
, такое, что для всех x, быть может, не равных a и удовлетворяющих неравенству  , выполняется условие
, выполняется условие  . Обозначается
. Обозначается  . (1)
. (1)
 .
. Модуль
Модуль  , или
, или  , следовательно,
, следовательно,  . Если из
. Если из  удалить точку a, то получим проколотую дельта-окрестность (рис. 1).
удалить точку a, то получим проколотую дельта-окрестность (рис. 1).
 .
. Из определения предела следует, что
Из определения предела следует, что 
 . Поведение функции
. Поведение функции  в точке
в точке  . Но
. Но  .
. . По определению
. По определению  можно найти
можно найти 
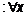 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , следовало бы
, следовало бы  . Преобразуем неравенство в
. Преобразуем неравенство в  или
или  . Тогда для любых
. Тогда для любых 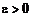 можно подобрать
можно подобрать  , то есть
, то есть  и
и  . Тогда, согласно определению предела,
. Тогда, согласно определению предела, 

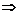
 и
и 

 . Примем за
. Примем за  и
и  =
= 

 . Тогда
. Тогда 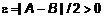 и оценим
и оценим 

 , т. е.
, т. е. 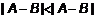 – противоречие, следовательно, предположение не верно и предел единственный.
– противоречие, следовательно, предположение не верно и предел единственный. – левая полуокрестность, т.е
– левая полуокрестность, т.е  .
. – правая полуокрестность, т.е
– правая полуокрестность, т.е  .
.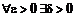

 .
.
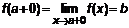 . Левосторонние и правосторонние пределы называются односторонними.
. Левосторонние и правосторонние пределы называются односторонними. . Доказать, что
. Доказать, что 
 . По определению 2 следует, что
. По определению 2 следует, что  следует
следует  , согласно (2)
, согласно (2)  . Аналогично
. Аналогично  , согласно (2)
, согласно (2)  .
.
 или
или  . Возьмем
. Возьмем  - любое положительное число. Тогда
- любое положительное число. Тогда  или
или  . Следовательно, все значения
. Следовательно, все значения  ). То же для отрицательного предела.
). То же для отрицательного предела. для любых
для любых  .
. - ограничена на R,
- ограничена на R, 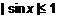 ,
,  на области определения не ограничена, а на отрезке
на области определения не ограничена, а на отрезке  - ограничена
- ограничена 
 , тогда по определению
, тогда по определению  . Следовательно,
. Следовательно,  или
или  . Обозначим
. Обозначим  , тогда
, тогда 
 , т. е. функция ограничена.
, т. е. функция ограничена. Определение 6.
Определение 6. , или
, или  . Обозначается
. Обозначается 
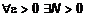

 . (3)
. (3) называется бесконечно малой функцией, или бесконечно малой величиной, в точке
называется бесконечно малой функцией, или бесконечно малой величиной, в точке  или
или  . (1)
. (1) – бесконечно малая величина в точках
– бесконечно малая величина в точках  и
и  .
. . Функция
. Функция 
 .
. , необходимо и достаточно, чтобы разность между
, необходимо и достаточно, чтобы разность между  . Необходимо доказать, что
. Необходимо доказать, что  . Из условия и определения предела следует, что
. Из условия и определения предела следует, что  . Следовательно,
. Следовательно, 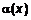 – бесконечно малая величина в точке
– бесконечно малая величина в точке  . Из того, что
. Из того, что  , или
, или  .
. есть бесконечно малая величина
есть бесконечно малая величина  - бесконечно малая величина в точке
- бесконечно малая величина в точке  , если
, если 
 .
. .
. , то согласно определению
, то согласно определению 


 . Если
. Если  , то согласно определению
, то согласно определению 

 . Для любых
. Для любых  . Для дельта-окрестности
. Для дельта-окрестности  =
= 
 оценим
оценим 

 , то есть
, то есть 
 и
и  – бесконечно малая величина. Для суммы n бесконечно малых величин с учетом предыдущего доказательство сводится к последовательному объединению слагаемых до случая суммы двух бесконечно малых величин.
– бесконечно малая величина. Для суммы n бесконечно малых величин с учетом предыдущего доказательство сводится к последовательному объединению слагаемых до случая суммы двух бесконечно малых величин. , то получим неопределенность
, то получим неопределенность  .
.  , то согласно определению
, то согласно определению  . Пусть функция
. Пусть функция  ,
, 

 . Примем
. Примем  =
= 
 , для которой выполняются предыдущие условия. Для любых
, для которой выполняются предыдущие условия. Для любых  . Оценим
. Оценим  . Таким образом,
. Таким образом,  ,
, 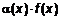 – бесконечно малая величина, т. е. если
– бесконечно малая величина, т. е. если  конечный предел, то
конечный предел, то  .
.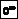 .
. ,
, 
 (неограниченная).
(неограниченная). или
или  . (2)
. (2) .
.  . Обозначим
. Обозначим  . Следовательно, согласно определению
. Следовательно, согласно определению  есть бесконечно большая величина.
есть бесконечно большая величина.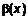 – бесконечно большая величина в точке
– бесконечно большая величина в точке  – бесконечно малая величина. По определению
– бесконечно малая величина. По определению  , или
, или  . Примем
. Примем 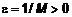 , тогда
, тогда 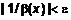
 .
. . Для сравнения этих величин находят
. Для сравнения этих величин находят . (3)
. (3) и
и  , то
, то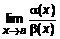 =
=  =
=  =
=  .
. , то говорят, что величины эквивалентны
, то говорят, что величины эквивалентны  , поскольку
, поскольку  и
и  ~
~  .
. ;
;