
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задачи, приводящие к понятию производной функции1.1. Скорость прямолинейного движения
Если в некоторый момент времени t точка занимает положение M, то в момент времени
 . .
Однако это средняя скорость за период времени
1.2 Касательная к кривой Возьмем на непрерывной кривой L две точки
Прямая, проходящая через две точки непрерывной кривой, называется секущей. Пусть точка Определение № 2. Касательной к данной кривой в данной точке M называется предельное положение секущей, проходящая через эту точку, когда вторая точка Рассмотрим график непрерывной кривой 
 . (2) . (2)
При
Читается: V равно S штрих по t или тангенс 2. Определение производной |
||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 630. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Пусть материальная точка (некоторое тело) M движется неравномерно по некоторой прямой, например, спортсмен, преодолевающий 100 м. Пусть нам известна зависимость пройденного расстояния
Пусть материальная точка (некоторое тело) M движется неравномерно по некоторой прямой, например, спортсмен, преодолевающий 100 м. Пусть нам известна зависимость пройденного расстояния  (рис. 1) от времени t в виде
(рис. 1) от времени t в виде  , то есть, известен закон движения точки.
, то есть, известен закон движения точки. точка займет положение
точка займет положение  , то есть за время
, то есть за время  расстояние точки изменится с
расстояние точки изменится с  на
на  . Таким образом, перемещение точки M за время
. Таким образом, перемещение точки M за время  . Найдем среднюю скорость материальной точки на этом интервале
. Найдем среднюю скорость материальной точки на этом интервале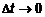 , получим скорость движения точки в данный момент времени, или мгновенную скорость. Обозначим эту скорость V и получим
, получим скорость движения точки в данный момент времени, или мгновенную скорость. Обозначим эту скорость V и получим . (1)
. (1) и
и  Определение № 1.
Определение № 1. (рис. 3), имеющий в точке
(рис. 3), имеющий в точке  невертикальную касательную. Найдем ее угловой коэффициент
невертикальную касательную. Найдем ее угловой коэффициент  , где
, где  – угол касательной с осью
– угол касательной с осью 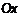 . Для этого проведем через точку
. Для этого проведем через точку 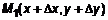 секущую
секущую  . Обозначим
. Обозначим  – угол между секущей и осью
– угол между секущей и осью  в силу непрерывности функции приращение
в силу непрерывности функции приращение 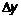 тоже стремится к нулю. Поэтому точка
тоже стремится к нулю. Поэтому точка 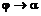 , т. е.
, т. е.  . Следовательно,
. Следовательно,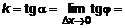
 . (3)
. (3) Итак, мы пришли к необходимости нахождения предела отношения приращения функции к пределу приращения аргумента. К нахождению пределов вида (1) и (2) приводят решения и множества других прикладных задач, будь то сила тока, скорость течения химической реакции, скорость роста популяции или экономический рост. В любом случае пределы будут иметь одинаковый вид. Эти пределы записываются кратко
Итак, мы пришли к необходимости нахождения предела отношения приращения функции к пределу приращения аргумента. К нахождению пределов вида (1) и (2) приводят решения и множества других прикладных задач, будь то сила тока, скорость течения химической реакции, скорость роста популяции или экономический рост. В любом случае пределы будут иметь одинаковый вид. Эти пределы записываются кратко или
или  .
.