
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференцирование обратной функцииТеорема 2. Если
Производная обратной функции равна обратной величине производной данной функции. Доказательство. 1. Аргументу 2. Найдем соответствующее приращение функции 3. Запишем отношение 4. Найдем предел ПРИМЕР 1. Дана
3.1. Дифференцирование суммы Теорема 3. Если функции
Доказательство. 1. Аргументу 2. Найдем соответствующее приращение функций 3. Запишем отношение 4. Найдем предел Следствие! Методом математической индукции можно доказать, что теорема верна для любого конечного числа слагаемых
3.2. Дифференцирование произведения Теорема 4.
 и и  дифференцируемы в некоторой точке, то функция дифференцируемы в некоторой точке, то функция  дифференцируема в той же точке и производная произведения равна сумме произведений первой функции на вторую и производной второй функции на первую дифференцируема в той же точке и производная произведения равна сумме произведений первой функции на вторую и производной второй функции на первую
Доказательство. 1. Аргументу 2. Найдем соответствующее приращение функций 3. Запишем отношение 4. Найдем Следствие! Теорема справедлива для любого числа сомножителей. Например, 3.3. Дифференцирование частного Теорема 5. Если функции
Доказательство. 1. Аргументу 2. Найдем соответствующее приращение функций 3. Запишем отношение 4. Найдем предел 4. Логарифмическое дифференцирование Определение 1.
ПРИМЕР 2. Найти производную Данный метод используется для степенно-показательных функций вида
1. Логарифмируем обе части уравнения 2. Дифференцируем обе части уравнения. Следовательно, 3. С учетом 5. Производные функций, заданных неявно и параметрически 5.1. Производная функции, заданной неявно Дифференцирование неявной функции схоже с логарифмическим дифференцированием, так как логарифмирование дает неявную функцию. Пусть функция y связана с аргументом x неявно, т. е.
Продифференцируем (7) по переменной x. С учетом того, что y – функция от x, будем применять указанные выше правила. Из полученного выражения Пусть задана функция неявно ПРИМЕР 3. Дана функция
Пусть функция y связана с аргументом x параметрически, т. е.
ПРИМЕР 4. Траектория движения точки задана параметрически 6. Производные высших порядков Пусть Определение 2.
 . .
Важно! Физический смысл второй производной: Определение 3. Производная от производной второго порядка называется производной второго порядка или третьей производной Определение 4. Производная от производной Все производные более второго порядка называются производными высших порядков. Заключение В лекции приведены некоторые примеры применения правил дифференцирования функций, производные которых будут изучаться в следующей лекции. Отметим что: - производная сложной функции равна произведению производной функции по промежуточной переменной на производную промежуточной переменной по независимой переменной; - производная обратной функции равна обратной величине производной данной функции; - производная произведения равна сумме произведений первой функции на вторую и производной второй функции на первую; - логарифмическое дифференцирование применяется для упрощения расчета и для нахождения производных степенно-показательных функций; - производная параметрически заданной функции равна отношению производных функции и переменной по параметру. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980. – 384 с. 2. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с.
Цель лекции: изучить основные производные элементарных функций, научиться применять их при решении задач с использованием правил дифференцирования. План лекции 1. Дифференцирование постоянной величины и независимой переменной 2. Производная степенной функции 3. Производная показательной функции 4. Производная логарифмической функции 5. Производные тригонометрических функций 6. Производные обратных тригонометрических функций 7. Производные гиперболических функций Введение На предыдущей лекции изучались правила дифференцирования функций. Для использования этих правил необходимо знать производные элементарных функций. Ранее при рассмотрении некоторых примеров уже применялись производные некоторых функций. Используя правила нахождения производных, можно получить основные производные элементарных функций. Их необходимо знать и уметь применять при решении прикладных задач. Указанные функции составляют таблицу производных. |
||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 775. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 дифференцируема и имеет обратную функцию
дифференцируема и имеет обратную функцию  , то обратная функция также дифференцируема, причем
, то обратная функция также дифференцируема, причем или
или  . (2)
. (2)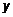 дадим приращение
дадим приращение 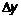 .
.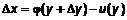 .
. .
. . Из необходимого условия дифференцируемости следует, что бесконечно малому приращению аргумента
. Из необходимого условия дифференцируемости следует, что бесконечно малому приращению аргумента  соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции  . Тогда последний предел перепишем в виде
. Тогда последний предел перепишем в виде  . Следовательно, существует предел левой части равенства, т. е. существует производная обратной функции.
. Следовательно, существует предел левой части равенства, т. е. существует производная обратной функции. . Тогда
. Тогда  и
и  .
. дифференцируема в той же точке и производная суммы равна сумме производных
дифференцируема в той же точке и производная суммы равна сумме производных . (3)
. (3) дадим приращение
дадим приращение  .
.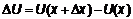 ,
,  и
и  .
.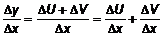 .
. . Два последних предела существуют по условию. Следовательно, выражение (3) справедливо.
. Два последних предела существуют по условию. Следовательно, выражение (3) справедливо. .
. . (4)
. (4) .
. .
.
 . Два последних предела существуют по условию. Следовательно, выражение (4) справедливо.
. Два последних предела существуют по условию. Следовательно, выражение (4) справедливо. .
. дифференцируема в той же точке, причем
дифференцируема в той же точке, причем . (5)
. (5) .
. .
.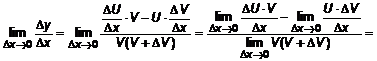
 . Два предела в числителе существуют по условию, а предел
. Два предела в числителе существуют по условию, а предел  в силу дифференцируемости
в силу дифференцируемости  . Следовательно, выражение (5) справедливо.
. Следовательно, выражение (5) справедливо. . Для упрощения применим логарифмическое дифференцирование. Прологарифмируем
. Для упрощения применим логарифмическое дифференцирование. Прологарифмируем 
 . Отметим, что на следующей лекции будет показано
. Отметим, что на следующей лекции будет показано  . Продифференцируем обе части уравнения
. Продифференцируем обе части уравнения  , откуда получим
, откуда получим  .
. , где
, где 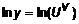 .
. , откуда
, откуда  .
. . (6)
. (6) . (7)
. (7) выразим
выразим  .
. , где
, где  и
и  – дифференцируемые функции. Тогда с учетом того, что y – функция от x , т.е.
– дифференцируемые функции. Тогда с учетом того, что y – функция от x , т.е. 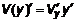 , получим
, получим  . Откуда
. Откуда  .
. . Определим
. Определим  , получим
, получим  . Откуда
. Откуда  .
. , (8)
, (8) и
и  – дифференцируемые функции. По условию функция
– дифференцируемые функции. По условию функция  , которая также дифференцируема
, которая также дифференцируема  . Подставим обратную функцию во второе уравнение системы (8) и получим
. Подставим обратную функцию во второе уравнение системы (8) и получим  . Тогда производная сложной функции
. Тогда производная сложной функции  , или
, или . (9)
. (9) Производная функции, заданной параметрически, равна отношению производной этой функции по параметру к производной аргумента по этому параметру.
Производная функции, заданной параметрически, равна отношению производной этой функции по параметру к производной аргумента по этому параметру. , где
, где  – начальная скорость движения, g – ускорение,
– начальная скорость движения, g – ускорение,  – начальный угол движения относительно оси
– начальный угол движения относительно оси 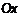 (рис. 1). Определим текущее направление движения, то есть угол наклона касательной
(рис. 1). Определим текущее направление движения, то есть угол наклона касательной  . Тогда
. Тогда  .
. . В свою очередь функция
. В свою очередь функция  может быть также дифференцируема, причем
может быть также дифференцируема, причем  .
. есть скорость изменения скорости, или ускорение.
есть скорость изменения скорости, или ускорение. .
. порядка называется производной n-го порядка, или n-ой производной
порядка называется производной n-го порядка, или n-ой производной  .
.