
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Критерий устойчивости Найквиста.⇐ ПредыдущаяСтр 27 из 27 Знаменатель передаточной функции на единицу отличающуюся от передаточной функции разомкнутой системы
Так как в реальных системах порядок оператора правой части дифференциального уравнения всегда меньше порядка оператора левой части дифференциального уравнения, т.е. степень многочлена Подставив в выражение (3.19) числитель и знаменатель из равенств (2.13) и (5.22) , получим передаточную функцию замкнутой системы
Многочлен
корни которого позволяют найти по формуле (2.38) общее решение однородного дифференциального уравнения системы. Следовательно, числитель функции Перейдем от оператора
Согласно формуле (5.22) частотная функция запишется так:
где В показательной форме можно записать: 
где
При изменении Для работоспособности системы необходимо, чтобы в рабочем (замкнутом) состоянии она была устойчивой. Это требование, согласно критерию устойчивости Михайлова выражается условием.
В разомкнутом состоянии в общем случае система может быть и неустойчивой, однако если в замкнутом рабочем состоянии она устойчива, то этого достаточно для ее нормальной работы. Принимая в общем случае, что в разомкнутом состоянии система неустойчива и ее характеристическое уравнение
Таким образом,
Так как выражение (5.26) обеспечивает отсутствие корней характеристического уравнения замкнутой системы справа от мнимой оси, то оно является необходимым и достаточным условием устойчивости системы и называется критерием устойчивости Найквиста. Если Критерий устойчивости Найквиста можно сформулировать следующим образом: Замкнутая линейная система устойчива, если приращение фазы функции
Рис.5.5. Амплитудно-фазовые характеристики а – устойчивые в замкнутом состоянии; б – неустойчивые в замкнутом состоянии.
|
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 470. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 замкнутой системы автоматического регулирования представляет собой функцию
замкнутой системы автоматического регулирования представляет собой функцию  , (5.21)
, (5.21) . С учетом выражения (2.6)
. С учетом выражения (2.6)  получим:
получим: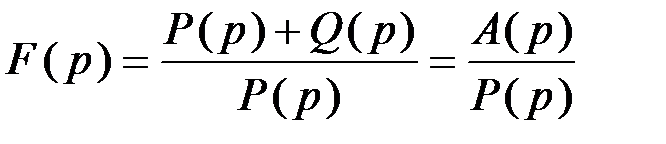 (5.22)
(5.22)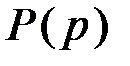 всегда больше степени многочлена
всегда больше степени многочлена  , то степени числителя и знаменателя
, то степени числителя и знаменателя  одинаковы и определяются степенью
одинаковы и определяются степенью 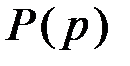 , равной
, равной  .
. . (5.23)
. (5.23) знаменателя передаточной функции есть характеристический многочлен дифференциального уравнения замкнутой системы, составляющий левую часть характеристического уравнения (2.37)
знаменателя передаточной функции есть характеристический многочлен дифференциального уравнения замкнутой системы, составляющий левую часть характеристического уравнения (2.37) ,
, является характеристическим многочленом
является характеристическим многочленом  передаточной функции замкнутой системы, а знаменатель
передаточной функции замкнутой системы, а знаменатель 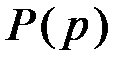 согласно формуле (2.6) – характеристическим многочленом разомкнутой системы.
согласно формуле (2.6) – характеристическим многочленом разомкнутой системы. в формуле (5.21), получим функцию
в формуле (5.21), получим функцию  , на единицу отличающуюся от амплитудно-фазовой характеристики разомкнутой системы
, на единицу отличающуюся от амплитудно-фазовой характеристики разомкнутой системы 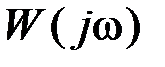 :
: . (5.24)
. (5.24) , (5.25)
, (5.25) – годограф Михайлова замкнутой системы;
– годограф Михайлова замкнутой системы; – годограф Михайлова разомкнутой системы.
– годограф Михайлова разомкнутой системы.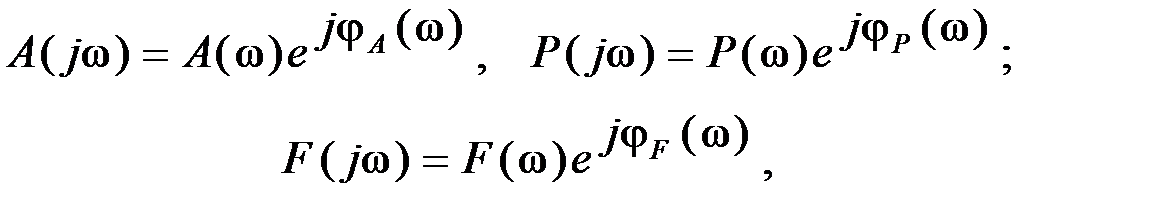
 .
. от 0 до
от 0 до  полное приращение фазы функции
полное приращение фазы функции  будет равно:
будет равно:  .
. .
. имеет
имеет 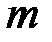 корней справа от мнимой оси, согласно формуле (5.18) (
корней справа от мнимой оси, согласно формуле (5.18) ( 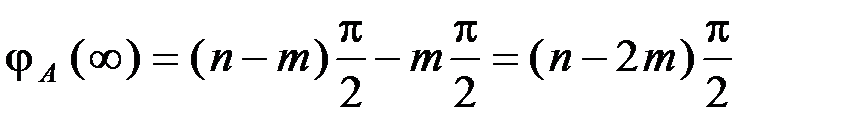 ) критерия Михайлова запишем:
) критерия Михайлова запишем: .
. . (5.26)
. (5.26)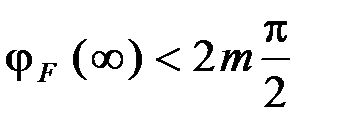 , то замкнутая система неустойчива.
, то замкнутая система неустойчива. при изменении
при изменении  от 0 до
от 0 до  будет равно
будет равно  , где
, где  – число корней характеристического уравнения разомкнутой системы, лежащих на комплексной плоскости справа от мнимой оси.
– число корней характеристического уравнения разомкнутой системы, лежащих на комплексной плоскости справа от мнимой оси.