
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Временные хар-ки. Единичная ф-ия. Переходная хар-ка.Динамические свойства звена могут быть определены по его переходной функции и функции веса. Переходная функция, или переходная характеристика Математическое выражение единичного ступенчатого воздействия может быть записано в виде:
Если входное воздействие представляет собой неединичную ступенчатую функцию Ступенчатая функция представляет собой распространенный вид входного воздействия в автоматических системах. К такому виду сводится мгновенное изменение нагрузки электрического генератора, мгновенное возрастание нагрузки на валу двигателя, мгновенный поворот командной оси следящей системы (оси прецессии гироскопа) и т.п. Умножение какой-либо функции времени
Функция веса
Импульсная функция или дельта-функция представляет собой производную от единичной ступенчатой функции: Основное свойство дельта-функции заключается в том, что  Из последнего выражения следует, что размерность дельта-функции равна [c-1]. При практических расчетах наиболее широкое применение находит временная характеристика в виде переходной характеристики, так как ее достаточно просто получить экспериментально и, кроме того, определяемый ею переходный процесс в системе часто возникает при включениях и изменении задания регулятору. Кроме того, использование ступенчатого постоянного или импульсного воздействия в виде стандартного входного сигнала имеет также то преимущество, что действительные, любой формы, возмущающие воздействия на систему можно представить в виде последовательности таких сигналов. Так, входной сигнал, изображенный на рис. 3.7, б, можно представить в виде суммы постоянных ступенчатых сигналов, то
Иначе где
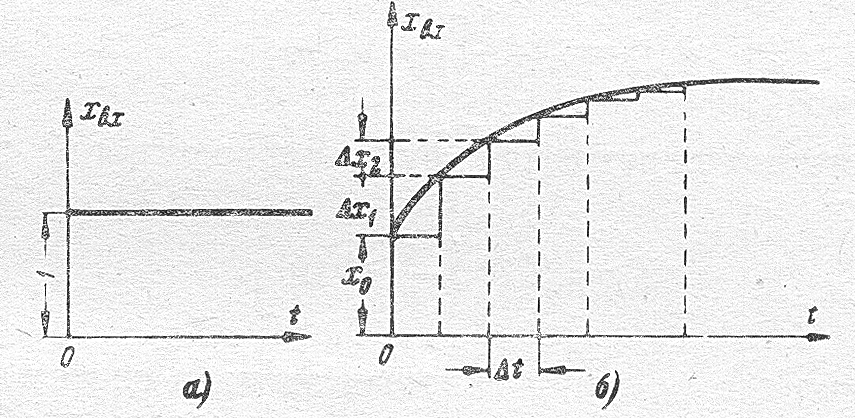
Просуммировав временные характеристики системы с учетом начального времени воздействия каждого скачка, а также их фактической величины, можно получить характер изменения выходной величины при входном воздействии по форме рис. 3.7, б.
Рис. 3.7. Пример интегрированного входного Для того чтобы получить выходное значение соответствующее не ступенчатой кривой, а заданному плавно изменяющемуся значению в соответствии с передаточной функцией системы, необходимо промежутки времени уменьшать до бесконечно малой величины Сумма в пределе перейдет в интеграл. Точное выходное значение для фиксированного момента времени
Полученное выражение называется интегралом Дюамеля. Поскольку согласно Приложению 1 входная и выходная величины в преобразованном по Лапласу виде запишется как:
поскольку
С учетом этого получим
|
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 527. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
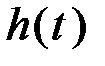 описывает переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице (рис. 3.5). Такое входное воздействие называется единичной ступенчатой функцией и обозначается
описывает переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице (рис. 3.5). Такое входное воздействие называется единичной ступенчатой функцией и обозначается 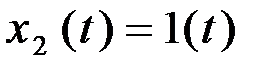 .
.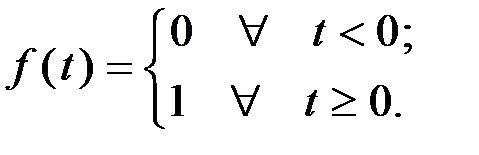
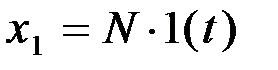 , выходная величина будет равна
, выходная величина будет равна 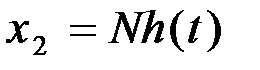 .
.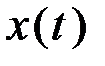 на единичную ступенчатую функцию
на единичную ступенчатую функцию 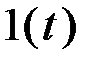 означает, что функция времени
означает, что функция времени 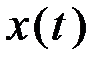 будет существововать только при
будет существововать только при 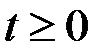 , при
, при 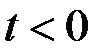 она обращается в нуль. Это иллюстрирует рис. 3.5.
она обращается в нуль. Это иллюстрирует рис. 3.5.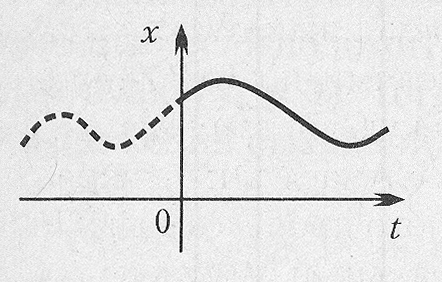
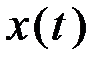
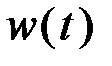 представляет собой реакцию звена на единичную импульсную функцию, поданную на его вход (рис. 3.6).
представляет собой реакцию звена на единичную импульсную функцию, поданную на его вход (рис. 3.6).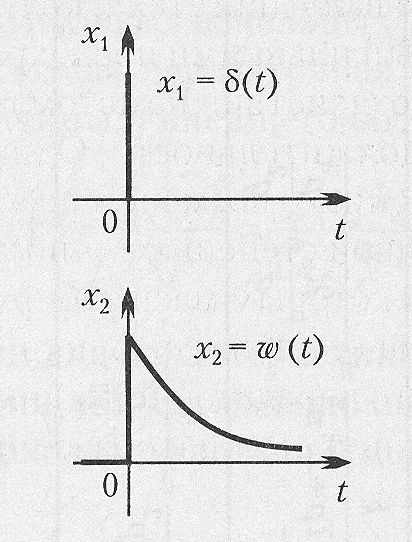 Рис. 3.6. Импульсная функция
Рис. 3.6. Импульсная функция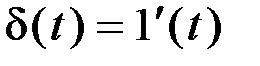 . Дельта-функция тождественно равна нулю повсюду, кроме точки
. Дельта-функция тождественно равна нулю повсюду, кроме точки 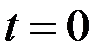 , где она стремится к бесконечности.
, где она стремится к бесконечности.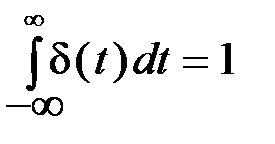 т.е. она имеет единичную площадь.
т.е. она имеет единичную площадь.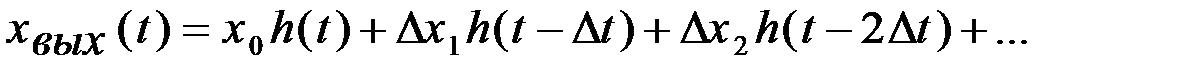
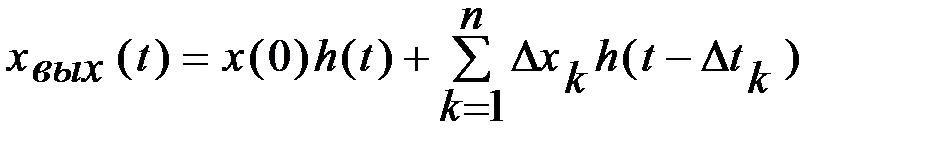 ,
,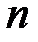 – число промежутков, на которое разбит интервал времени от 0 до
– число промежутков, на которое разбит интервал времени от 0 до 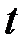 .
.
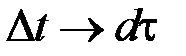 , а число скачков
, а число скачков 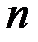 увеличивать до бесконечности (
увеличивать до бесконечности ( 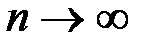 ). Сами скачки при этом будут бесконечно малыми величинами. Величину каждого скачка
). Сами скачки при этом будут бесконечно малыми величинами. Величину каждого скачка 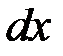 можно представить в виде произведения скорости изменения
можно представить в виде произведения скорости изменения 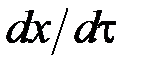 на продолжительность этого промежутка
на продолжительность этого промежутка 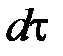 , т.е.
, т.е. 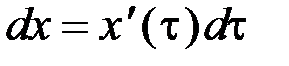 .
. можно записать:
можно записать: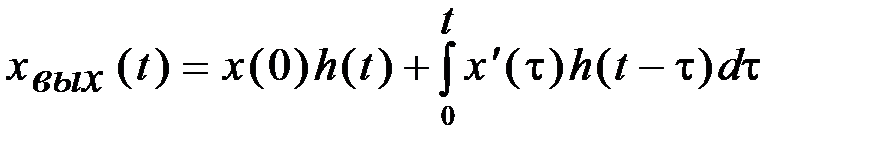
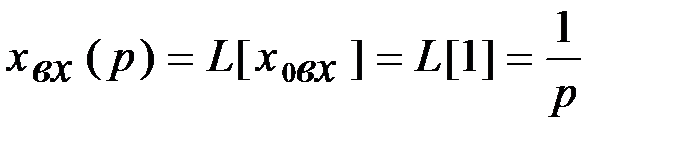 ;
;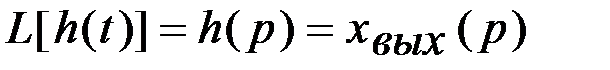 ,
,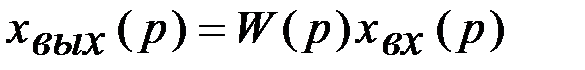 .
.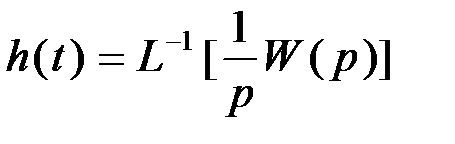 .
.