
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Динам хар-ки типовых звеньев и их звеньев. Инерц звено 2-го порядка.В соответствии с передаточной функцией инерционного звена второго порядка
АФХ можно записать в виде: Вещественная частотная характеристика Мнимая частотная характеристика Амплитудно-частотная характеристика Фазо-частотная характеристика На рис. 3.20 изображена амплитудно-фазовая характеристика (АФХ) звена.
Рис. 3.20. АФХ инерционного звена второго порядка при разном отношении АФХ начинается на действительной оси в точке с абсциссой, равной При
и имеет вид окружности с радиусом При При этом, чем меньше При Амплитудно-фазовая характеристика при этом определяется выражением Графически эта характеристика при изменении частоты колебаний входной величины  Определяя первую производную АЧХ по частоте и приравнивая полученное выражение нулю, находим:
Отсюда вытекает, что
или Из этого уравнения находим значение частот, при которых АЧХ имеет экстремумы:
Из выражения для АЧХ следует, что при
и не зависит от величины постоянных времени Второе вещественное экстремальное значение
При этом чем больше отношение постоянных времени приближается к значению Рассмотрим второй экстремум кривой
при дальнейшем увеличении частоты АЧХ стремится к нулю.
Рис. 3.21 Амплитудно-частотные характеристики инерционного звена второго порядка Если продолжить дальнейшее уменьшение отношения При Итак, если входная величина является постоянной ( Из рисунка 3.21, б видно, что всё семейство характеристик При
|
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 466. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |




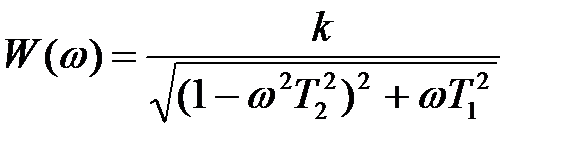



 . Вид АФХ определяется величиной отношения постоянных времени
. Вид АФХ определяется величиной отношения постоянных времени  . Чем больше это отношение, тем меньше колебательность звена. При
. Чем больше это отношение, тем меньше колебательность звена. При  колебательное звено превращается в соединение из двух апериодических звеньев первого порядка.
колебательное звено превращается в соединение из двух апериодических звеньев первого порядка. и
и  отношение
отношение  , а инерционное звено второго порядка превращается в инерционное звено первого порядка с постоянной времени
, а инерционное звено второго порядка превращается в инерционное звено первого порядка с постоянной времени  . Амплитудно-фазовая характеристика в этом случае определяется выражением
. Амплитудно-фазовая характеристика в этом случае определяется выражением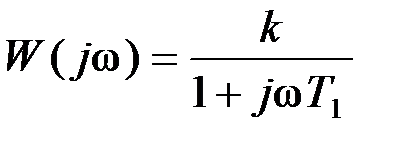 ,
, , центр которой расположен на вещественной оси в точке (
, центр которой расположен на вещественной оси в точке (  ).
). инерционное звено второго порядка превращается в колебательное звено (соотношение 2.49).
инерционное звено второго порядка превращается в колебательное звено (соотношение 2.49).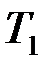 , тем меньше отношение
, тем меньше отношение  и тем меньше степень затухания колебаний в звене (соотношение (2.51).
и тем меньше степень затухания колебаний в звене (соотношение (2.51). степень затухания
степень затухания  будет равна нулю и возникшие в звене колебания будут незатухающими с собственной частотой колебаний, равной
будет равна нулю и возникшие в звене колебания будут незатухающими с собственной частотой колебаний, равной  .
. . (3.31)
. (3.31) имеет вид двух полупрямых
имеет вид двух полупрямых  на вещественной положительной полуоси в точке
на вещественной положительной полуоси в точке  и при возрастании
и при возрастании  уходит в бесконечность по вещественной полуоси в положительном направлении. Вторая полупрямая совпадает с отрицательной вещественной полуосью. Начало прямой в бесконечности при
уходит в бесконечность по вещественной полуоси в положительном направлении. Вторая полупрямая совпадает с отрицательной вещественной полуосью. Начало прямой в бесконечности при  , а конец – в начале координат при
, а конец – в начале координат при  , т.е. функция не определена и терпит разрыв на частоте
, т.е. функция не определена и терпит разрыв на частоте  . Такой разрыв графически представляют окружностью бесконечного радиуса, а функцию для практического использования доопределяют затуханием
. Такой разрыв графически представляют окружностью бесконечного радиуса, а функцию для практического использования доопределяют затуханием 

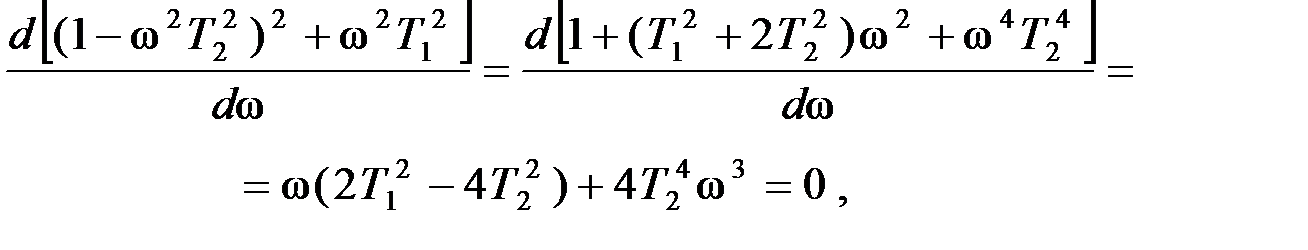

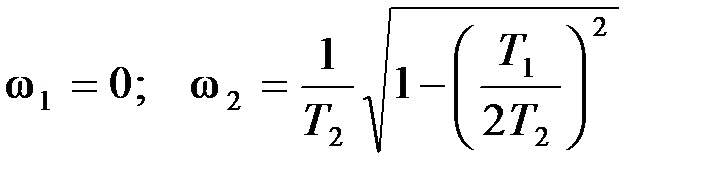
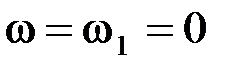 АЧХ равна коэффициенту усиления инерционного звена второго порядка:
АЧХ равна коэффициенту усиления инерционного звена второго порядка: ,
, ,
,  и их соотношения.
и их соотношения. имеется только при
имеется только при .
. , тем ближе подходит вторая точка экстремума к первой (это видно из рис. 3.21, а).
, тем ближе подходит вторая точка экстремума к первой (это видно из рис. 3.21, а). , появляющийся при
, появляющийся при  . Из рисунка видно, (и это можно аналитически показать на АЧХ), что при возрастании
. Из рисунка видно, (и это можно аналитически показать на АЧХ), что при возрастании  от
от  до
до  АЧХ также возрастает, начиная со значения
АЧХ также возрастает, начиная со значения  , и при
, и при  достигает максимального значения:
достигает максимального значения: ,
,
 и фазочастотные
и фазочастотные 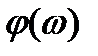
 , максимум АЧХ увеличивается и приближается к собственной частоте колебаний звена
, максимум АЧХ увеличивается и приближается к собственной частоте колебаний звена  .
. максимум
максимум 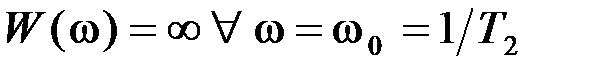 . Амплитудно-частотная характеристика при этом совпадает с амплитудно-фазовой и определяется выражением (3.31).
. Амплитудно-частотная характеристика при этом совпадает с амплитудно-фазовой и определяется выражением (3.31). ), то
), то  . Если частота входной величины стремится к бесконечности, то амплитудно-частотная характеристика стремится к нулю, что явствует из рисунка.
. Если частота входной величины стремится к бесконечности, то амплитудно-частотная характеристика стремится к нулю, что явствует из рисунка.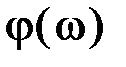 для различных отношений
для различных отношений  равно нулю при
равно нулю при  , равно
, равно  при частоте
при частоте  и стремится к
и стремится к  при частоте
при частоте  . Так как
. Так как  отрицательна, то выходные колебания во всем диапазоне изменения
отрицательна, то выходные колебания во всем диапазоне изменения  отстают от входных колебаний.
отстают от входных колебаний. фаза выходных колебаний совпадает с фазой входных колебаний в диапазоне изменений
фаза выходных колебаний совпадает с фазой входных колебаний в диапазоне изменений  от
от 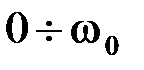 . При
. При  происходит изменение фазы скачком от
происходит изменение фазы скачком от  до
до  , и в диапазоне изменения
, и в диапазоне изменения  от
от  фаза выходных колебаний отстает от фазы входных колебаний на
фаза выходных колебаний отстает от фазы входных колебаний на 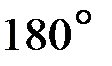 .
. 