
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Соединения статических элементовСтатическая характеристика системы, образованной соединением двух элементов, может быть найдена двумя способами: · аналитическим, если заданы формулы статических характеристик исходных элементов; · графическим, если характеристики элементов заданы графиками. Рассмотрим основные типы соединений статических элементов и методы аналитического и графического расчета их статических характеристик. · Параллельное соединение (рис. 3.2, а):
Рис.3.2.Графическоепостроение результирующей характеристики
· Последовательное соединение (рис. 3.3, а):
Графическое построение результирующей характеристики · на оси абсцисс характеристики первого элемента выбираем значение · рассматривая · для каждой пары чисел Нелинейные элементы нельзя переставлять местами, т.к. в общем случае
Например, для функций
· Соединение с обратной связью (рис. 3.4, а). На рисунке и формулах в обозначениях «
Рис. 3.3. Графическое построение  Запишем уравнение трех блоков системы:
Исключая переменные
Оно имеет решение в виде функции, обратной к статической характеристике
Аналитическое обращение нелинейной функции не всегда возможно. Так, для функции
Откуда видно, что явной зависимости
Рис. 3.4. Соединение с обратной связью
Последовательность графического построения статической характеристики обратного соединения
дает функцию
|
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 590. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
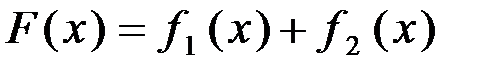 . Графическое построение результирующей характеристики
. Графическое построение результирующей характеристики 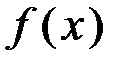 очень просто: она равна сумме ординат
очень просто: она равна сумме ординат 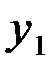 и
и 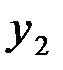 характеристик, параллельно соединенных элементов при одинаковых значениях абсцисс
характеристик, параллельно соединенных элементов при одинаковых значениях абсцисс 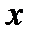 (рис. 3.2, б).
(рис. 3.2, б).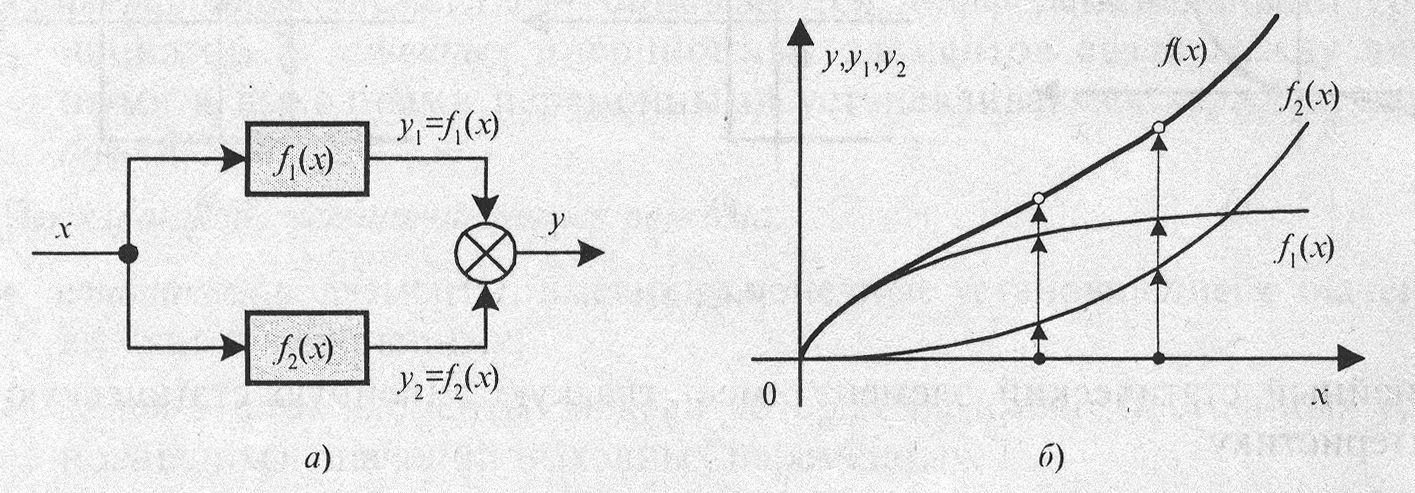
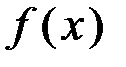
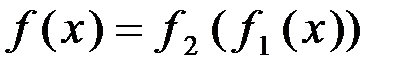 .
.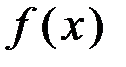 выполняется следующим образом (рис. 3.3, б):
выполняется следующим образом (рис. 3.3, б):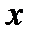 и по графику
и по графику 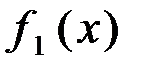 определяем выходной сигнал
определяем выходной сигнал 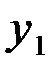 ;
;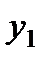 как входной сигнал второго элемента, по графику
как входной сигнал второго элемента, по графику 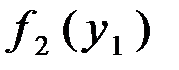 находим значение
находим значение 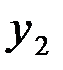 , равное выходному сигналу
, равное выходному сигналу 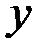 последовательного соединения. При этом ось
последовательного соединения. При этом ось 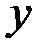 совпадает с осью
совпадает с осью 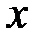 ;
;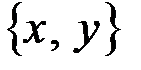 на отдельном графике строим точку искомой характеристики
на отдельном графике строим точку искомой характеристики 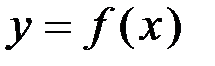 .
.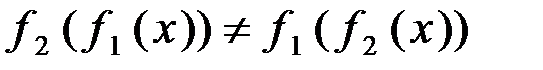 .
.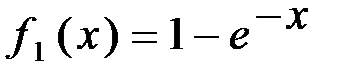 и
и 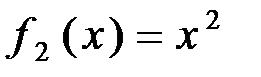 имеем
имеем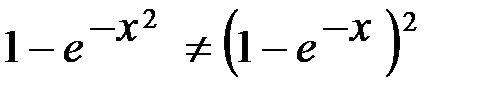 .
.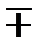 » верхний знак означает отрицательную обратную связь (ООС), а нижний положительную (ПОС).
» верхний знак означает отрицательную обратную связь (ООС), а нижний положительную (ПОС).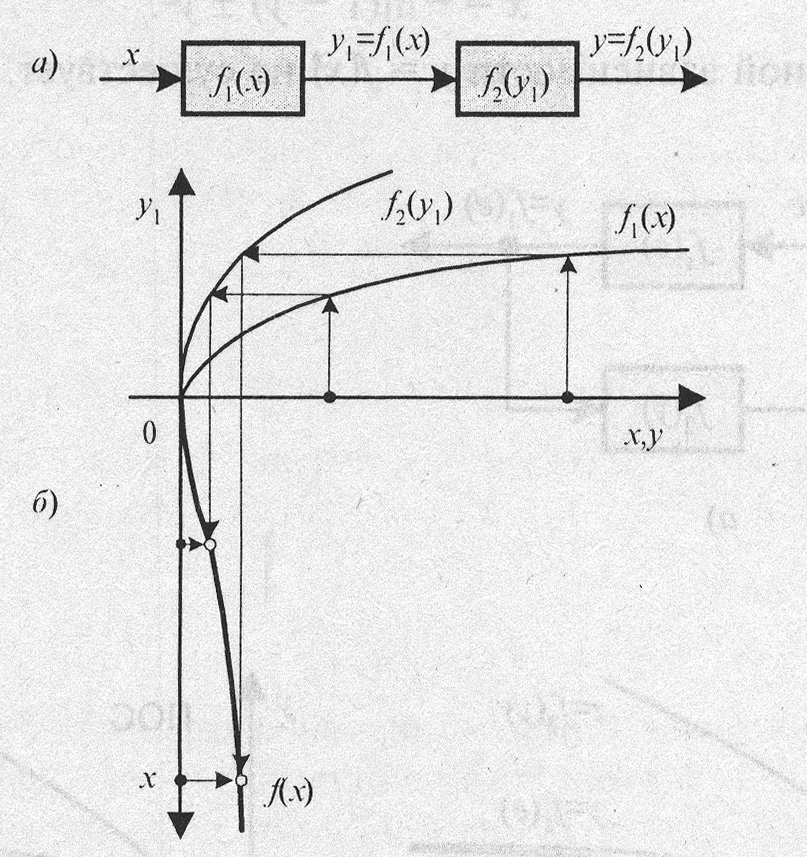
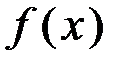
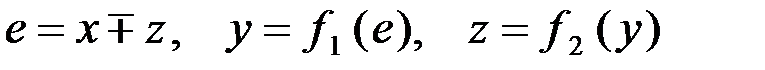 .
.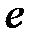 и
и 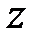 , получим уравнение связи входа и выхода:
, получим уравнение связи входа и выхода: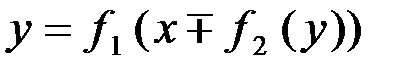 .
.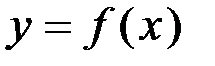 :
: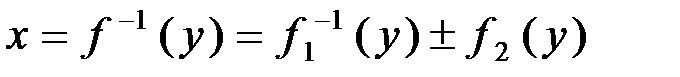 .
.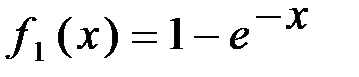 и
и 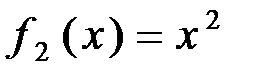 получим
получим 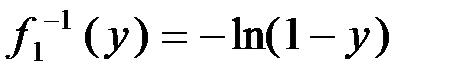 , откуда следует обратная зависимость
, откуда следует обратная зависимость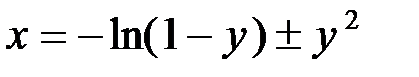 .
.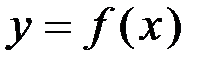 не существует.
не существует.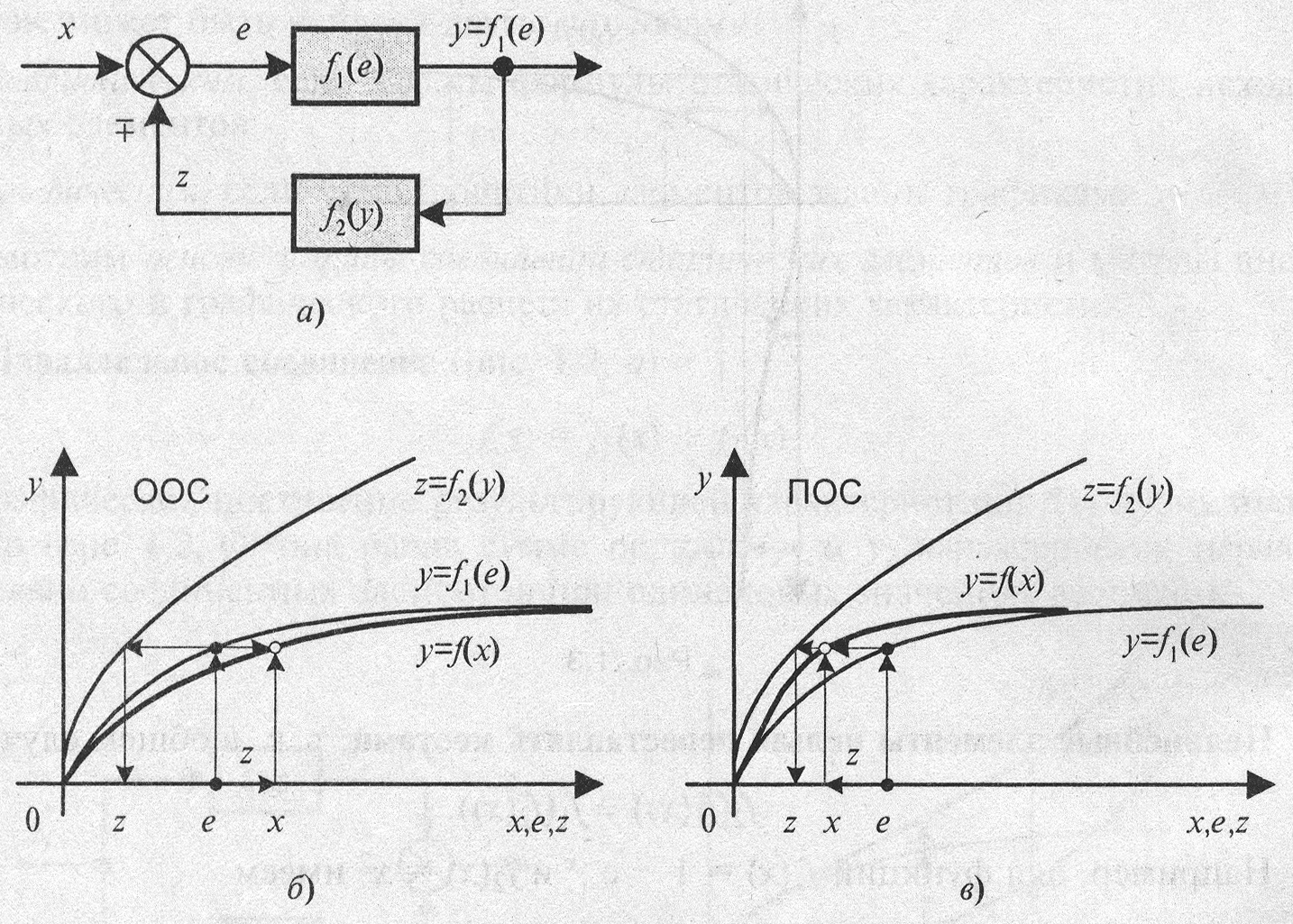
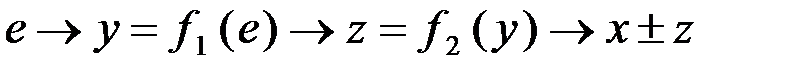
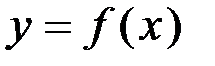 для каждого значения
для каждого значения 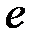 , и показана стрелками для случаев отрицательной (рис. 3.4, б) и положительной
, и показана стрелками для случаев отрицательной (рис. 3.4, б) и положительной