
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Пологая в общем случае, что динамический момент является функциейскорости, т. е. Мдин(w), время переходного процесса tп.п. при изменении скорости от w1 до w2 находим из основного уравнения движения электропривода
Интеграл в (1.325) можно взять только для частных случаев функции Мдин(w): а)Мдин(w) = Мдин= const, в этом случае
б)Мдин =
Поскольку электромеханическая постоянная времени TM определяется как
ОПТИМАЛЬНОЕ ПЕРЕДАТОЧНОЕ ЧИСЛО РЕДУКТОРА 1) По минимуму времени переходного процесса: a) (ЭДМ=const, Jд=const) (Исполн-й мех-м Mн,wн,Jн)
+ торможение , - разгон
При оптимальном j и отсуствия момента нагрузки на валу, кинетическая энергия механизма = кинетической энергии ЭД вместе с редуктором ОПТИМАЛЬНОЕ ПЕРЕДАТОЧНОЕ ЧИСЛОПО КРИТЕРИЮ минимум габарита ЭД угловое ускорение: при отсуствии нагрузки на выходном валу фиктивный момент инерции тогда МЕХАНИЧЕСКИЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ ПРИ ЛИНЕЙНОМ ДИНАМИЧЕСКОМ МОМЕНТЕ. В общем случае линейный динамический момент можно представить зависимостью
Мк – момент электродвигателя при w = 0, Мс – статический момент при w = 0, b – жесткость характеристики Мдин(w). Учитывая, что жесткость b характеристики Мдин(w) может быть положительной (кривая 1 на рис.1.26) или отрицательной (кривая 2 на рис.1.26), уравнение динамического момента удобнее записать таким образом
Подставляем (1.307) в основное уравнение движения электропривода  Обозначив Тм= получим неоднородное дифференциальное уравнение первого порядка с постоянными коэффициентами решение которого записывается в виде
где А - постоянная интегрирования, которая определяется из начальных условий, J – суммарный момент инерции электропривода, Тм– электромеханическая постоянная времени электропривода, wу – установившееся значение скорости , соответствующее Мдин= 0. Принимая скорость при t = 0 равной wнач, из (1.312) находим постоянную интегрирования А = wнач - wу (1.313) и окончательное уравнение скорости электропривода в переходном процессе w = (wнач- wу) Находим производную от (1.314): и подставляем в (1.315): М = Мс± Из (1.309) следует, что Поскольку (см. рис. 1.26) то уравнение (1.318) принимает вид Здесь, как и в (1.314) , знак плюс соответствует b> 0 , а минус - b< 0. В общем случае статический момент Мс может зависеть от скорости w , тогда при расчете электромагнитного момента М двигателя в (1.320) подставляется значение Мс , определяется для каждого момента времени t в (1.314) , используя кривую Мс(w). Уравнения (1.314) и (1.320) при b< 0 иллюстрируется кривыми, приведенными на рис. 1.27.
w = (0, 95¸0, 98)wу. Электромеханическую постоянную времени Тм можно определить графически (см. рис. 1.27). Действительно, из (1.314) имеем т. е. электромеханическая постоянная времени численно равна длине подкасательной РT. Аналогично, Тм можно получить из уравнения электромагнитного момента (1.320):
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 617. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

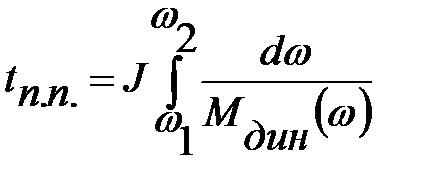 . (1.325)
. (1.325) , где
, где  .
. ±½b½w, тогда
±½b½w, тогда . (1.327)
. (1.327) , то время переходного процесса лучше представить в виде двух формул в зависимости от знака жёсткости
, то время переходного процесса лучше представить в виде двух формул в зависимости от знака жёсткости  динамического момента.
динамического момента. , при b> 0 (1.328)
, при b> 0 (1.328)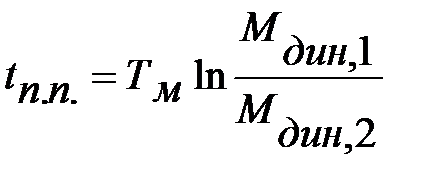 , при b< 0 (1.329)
, при b< 0 (1.329)

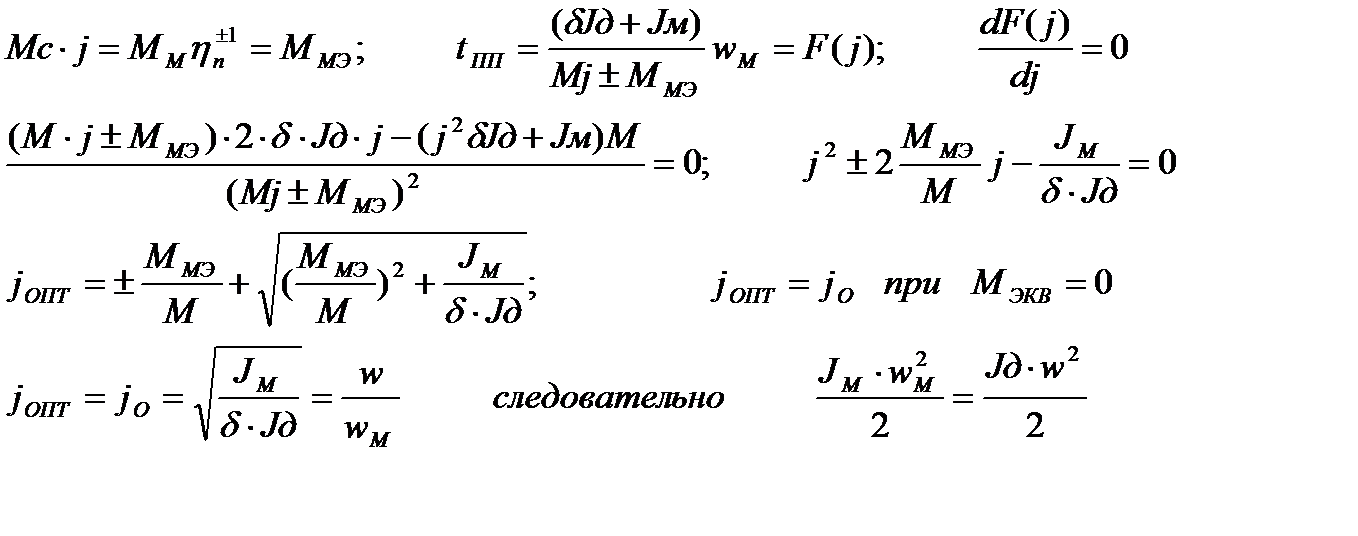

 ,
, ,
, следовательно
следовательно 

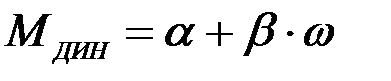 , (1.304) где
, (1.304) где  , (1.305)
, (1.305) , (1.306)
, (1.306) Мдин=
Мдин=  ±½b½w. (1.307)
±½b½w. (1.307) ±½b½w.=J
±½b½w.=J  (1.308)
(1.308) , (1.309)
, (1.309)  , (1.310)
, (1.310) , (1.311)
, (1.311) , (1.312)
, (1.312) +wу. (1.314) М=М с +Мдин = Мс+ J
+wу. (1.314) М=М с +Мдин = Мс+ J  . (1.315)
. (1.315) (1.316)
(1.316) . (1.317)
. (1.317) , тогда
, тогда  (1.318)
(1.318) , (1.319)
, (1.319) (1.320)
(1.320) Теоретически время переходного процесса равно бесконечности, практически принимают tп.п.= (3¸4)Тм, что соответствует достижению скорости
Теоретически время переходного процесса равно бесконечности, практически принимают tп.п.= (3¸4)Тм, что соответствует достижению скорости , (1.321)
, (1.321) (1.322)
(1.322)