
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Пример исходных формул и данных при априорной оценке точностиИсходные данные. Выполняя априорную оценку точности, необходимо задать ошибки градиентометра, если измерения производятся с градиентометром на борту ИСЗ или ошибки измеряемых величин(координат, расстояний, скоростей и так далее), если измерения производят в системе «спутник-спутник». Мы их возьмем из проекта CNES/ESA GRADIO (инструмент А. Бернарда). Ошибки градиентометра в этом проекте составляют ma=10-2EV (Этвеш), а в системе СИ это будет (1EV=10-9м/с2) ma=10-11мс-2 для градиентометра. Для системы «спутник-спутник» возьмем mr»30mm, mn»10-5mm×c-2. Гравитационный потенциал представим в виде: где а r, j, l геоцентрические, сферические координаты пробной массы (спутник, пробная масса градиентометра и т.д.), m – гравитационная постоянная, r0 – средний экваториальный радиус Земли и Возмущающую функцию R для дальнейших действий необходимо выразить через элементы орбиты. С этой целью воспользуемся каноническими элементами Делонэ: L, G, H, l, g, h.Элементы Делонэ связаны с кеплеровскимиэлементами a, ek, i, t, w, W следующими формулами: Обратные соотношения имеют вид: Возмущающая функция, выражая через эти элементы, имеет вид: где dmo – символы Кронера В свою очередь где Так как для спутниковой градиентометрии используют близкруговые орбиты (e~0,01 – 0,001), то для целей оценки достаточно ограничиться членами пропорциональными  |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 540. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
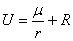 , (5.84)
, (5.84)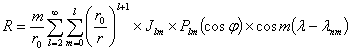 , (5.85)
, (5.85)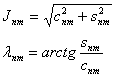 – стоксовы постоянные. (5.86)
– стоксовы постоянные. (5.86)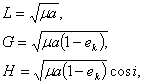
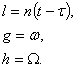 (5.87)
(5.87)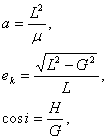
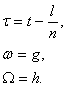 (5.88)
(5.88)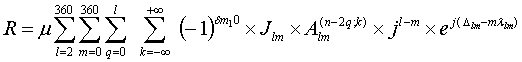 ,(5.89)
,(5.89)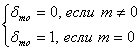 ,
, 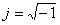 , е – основание натурального логарифма, Jnm и lnm – постоянные, связанные с классическими Сnm и Snm формулами (5.86),
, е – основание натурального логарифма, Jnm и lnm – постоянные, связанные с классическими Сnm и Snm формулами (5.86), 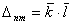 , где
, где  – целочисленный вектор, а
– целочисленный вектор, а 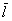 – вектор быстрых переменных и они имеют вид
– вектор быстрых переменных и они имеют вид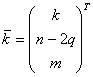 , а
, а 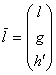 . (5.90)
. (5.90)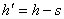 , где s – гринвичское звездное время. Функция от медленных переменных
, где s – гринвичское звездное время. Функция от медленных переменных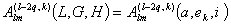 (5.91)
(5.91)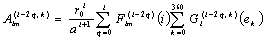 , (5.92)
, (5.92)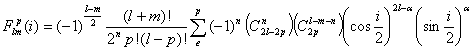 ,а (5.93)
,а (5.93)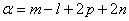 (5.94)
(5.94)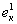 , а эти коэффициенты могут быть получены с помощью гипергеометрического ряда.
, а эти коэффициенты могут быть получены с помощью гипергеометрического ряда.