
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Общие принципы априорной оценки точностиАприорная (a priori –из предшествующего опыту, до опыта) оценка точности различного рода измерений выполняется на математических моделях, в которых заданы ошибки предполагаемых измерений заранее, ещё до того, как эти измерения будут выполнены. Поставим задачу по заданным ошибкам измерений (координат, скоростей и ускорений) и имеющимся уравнениям измеренных величин (это уравнения (5.21), (5.54) и (5.69) для различных моделей измеренных величин: разностей ускорений, расстояний, радиальных скоростей и ускорений) найти зависимость между ошибками вышеперечисленных величин и ошибками гравитационного поля Земли ΔSlm и ΔClm или ΔJlm и Δλlm. Обозначим обобщенно коэффициенты гравитации поля Земли ΔSlm, ΔClm или ΔJlm и Δλlm через Введем также следующие обозначения: Значениям промежуточных величин (элементам орбиты или другим каким–либо величинам) присвоим индекс (0) вверху, что будет означать полученные из наблюдений (observation), хотя некоторые из них и будут получены в результате вычислений, но все эти величины должны зашумляться заранее заданными моделями ошибок. Эта предпосылка обусловлена тем, что мы полагаем основным источником ошибок – неточное знание гравитационного поля Земли. Всем вычисленным значениям, на основании приближенной модели геопотенциала, присваивают индекс (С) (calculation). Отметим, что согласно введенным обозначениям, гравитационные постоянные ΔSlm, ΔClm или ΔJlm и Δλlm обобщенно можно записать так где приближенными, неточными значениями параметров гравитационного поля соответствует  Тогда мы можем произвольную зависимость измеренных величин и параметров разложить в ряд Тейлора в окрестности приближенных значений членами, где в выражении (5.61) предполагают известными на любой момент t приближенные значения координат Здесь обозначены операторы набла по разным переменным. Выражение (5.76) и(5.78) являются линейными уравнениями измеренных величин имеем следующее уравнения поправок: где Полагая, что мы имеем дело только со случайными ошибками, тогда сумма квадратов случайных величин, как известно, всегда равна нулю, то есть Найдя от этой функции минимум, получают нормальные уравнения, которые в последующем и дают зависимость между случайными ошибками всех измеряемых и искомых величин, входящих в (5.80) . Например, для второго уравнения (5.80) имеем нормальные уравнения которые служат исходными для получения зависимостей между средне-квадратическими ошибками измеряемых и искомых величин. В вышеприведенных выражениях полагают, что мы имеем дело с равноточными измерениями, когда матрица весовых коэффициентов равна 0. При оценке точности уравнение (5.81) нам даёт формулу для оценки точности где Формулы (5.71)-(5.73) являются примером уравнений измеренных величин и уравнений поправок, когда измеряются расстояния, скорости и ускорения в системе «спутник-спутник». Эти формулы получены Rummel K. и ReinbergK.H. и приводятся в их трудах. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 697. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
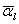 .
. – все наблюдаемые значения
– все наблюдаемые значения 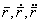
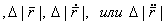 .
.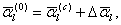 (5.75)
(5.75)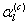 , т.е. заданные на основании приближенной модели гравитационного поля Земли.
, т.е. заданные на основании приближенной модели гравитационного поля Земли.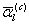 . Имеем, ограничиваясь линейными
. Имеем, ограничиваясь линейными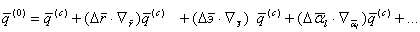 , (5.76)
, (5.76)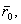 скоростей
скоростей 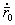 и ускорений
и ускорений 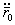 , а также элементов орбиты
, а также элементов орбиты 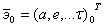 и приближенную модель гравитационного поля Земли
и приближенную модель гравитационного поля Земли 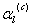 . В выражении (5.76) приняты следующие обозначения:
. В выражении (5.76) приняты следующие обозначения: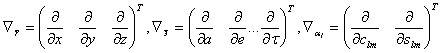 , (5.77)
, (5.77)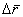 и
и 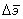 – это разности координат и элементов орбиты одного спутника относительно другого. Если мы будем полагать, что главные ошибки вносит гравитационное поле, а ошибками измеряемых величин можно пренебречь, то выражение (5.76) приобретает более простой вид
– это разности координат и элементов орбиты одного спутника относительно другого. Если мы будем полагать, что главные ошибки вносит гравитационное поле, а ошибками измеряемых величин можно пренебречь, то выражение (5.76) приобретает более простой вид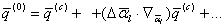 (5.78)
(5.78)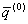 и они служат исходными уравнениями для получения уравнений поправок. В самом деле, обозначив через
и они служат исходными уравнениями для получения уравнений поправок. В самом деле, обозначив через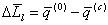 , (5.79)
, (5.79)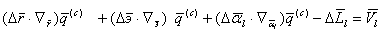 , или
, или 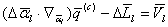 (5.80)
(5.80)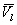 – вектор поправок, вызываемый только случайными ошибками.
– вектор поправок, вызываемый только случайными ошибками.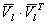 =0.
=0.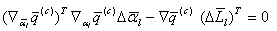 , (5.81)
, (5.81)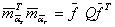 , (5.82)
, (5.82)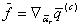
 ,а
,а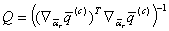 . (5.83)
. (5.83)