
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение элементов полного тензора градиентометрииИспользовав в качестве исходного уравнения движения для вращающегося вокруг центра масс спутника (5.16) и проделав преобразования, аналогичные тем, которые были использованы выше при выводе уравнения движения в инерциальной системе координат (5,7), получим дифференциальные уравнения движения произвольной точечной массы m, вращающейся вокруг центра масс спутника Правила действия с оператором где функция С учетом полученных выражений (5.18),(5.19) ,уравнение (5.17) принимает следующий вид: Распишем уравнение (5.20) в матричном виде. Оно будет иметь следующий вид Уравнения (5.20) и (5.21)) представляют собой систему дифференциальных уравнений второго порядка, состоящую из девяти уравнений. Первое слагаемое есть тензор гравитационного поля Земли, а все выражение получило название полного тензора градиентометрии. Элементами тензора гравитационного поля Земли являются вторые производные от потенциала Земли, Элементами полного тензора градиентометрии являются слагаемые из вторых производных геопотенциала и различных комбинаций угловых скоростей Свойства полного тензора градиентометрии и преобразование тензора гравитационного поля Земли Полный тензор градиентометрии имеет следующие базовые соотношения:  – Полусумма полного и транспортированного тензора градиентометрии дает следующее соотношение: – Полуразность тех же соотношений дает: Распишем выражение (5.23) подробнее: Выражение (5.24) дает только три линейно независимых уравнения, а именно На основании выражений (5.25) можно проводить априорный анализ о необходимости учета изменений угловых скоростей – По свойству оператора Лапласа Ñ2 сумма диагональных элементов тензора гравитационного поля Земли равна нулю, т.е.: Напомним, что выражение (5.26) (уравнение Лапласа) дает одну из четырех зависимостей между элементами тензора гравитационного поля Земли. Остальные три получаются из свойства безвихревого поля (гл.1.п.1.2.7), в котором ротор такого поля равен нулю. – Если сложить диагональные элементы левой части уравнений (5.21) и учесть уравнение Лапласа (5.26), то получим следующее выражение: – Переход от одной декартовой системы к другой выполняется по правилам преобразования тензоров второго ранга для матриц |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 612. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (5.17)
(5.17) над простейшими функциями от радиус–вектора
над простейшими функциями от радиус–вектора 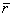 позволяет упростить выражение (5.17). А именно:
позволяет упростить выражение (5.17). А именно: , (5.18)
, (5.18) не зависит от
не зависит от  (5.19)
(5.19) . (5.20)
. (5.20) (5.21)
(5.21) ,
,  и т.д.
и т.д. и угловых ускорений
и угловых ускорений  . Заметим, что величины изменения скоростей весьма малы и при соответствующей предварительной их оценки в подавляющем большинстве их не учитывают.
. Заметим, что величины изменения скоростей весьма малы и при соответствующей предварительной их оценки в подавляющем большинстве их не учитывают. (5.22)
(5.22) (5.23)
(5.23) (5.24)
(5.24) (5.25)
(5.25) (5.26)
(5.26)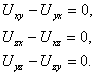 (5.27)
(5.27) (5.28)
(5.28) и
и 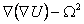 , и если
, и если  матрица преобразования при переходе от системы 1 к системе 2 ,то преобразования выполняются по формулам
матрица преобразования при переходе от системы 1 к системе 2 ,то преобразования выполняются по формулам  и
и 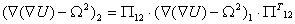 .
.