
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вывод уравнения движения для системы «спутник–спутник», когда измеряются расстояния, скорости и ускорения (Общий случай – разные орбиты)
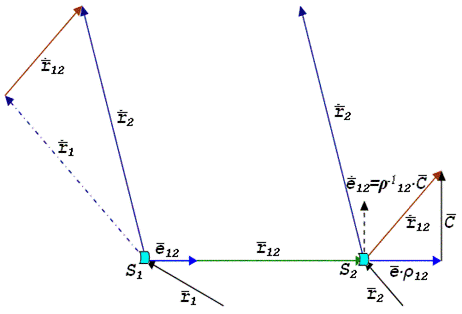
На рис.5.3 S1 и S2 изображены 2 спутника, расположенные на разных орбитах. Мгновенные положения их определяют радиусы–векторы Из рис.5.3 имеем Введем обозначения Взаимную скорость между спутниками можно представить в виде скалярного произведения где В самом деле, продифференцировав очевидное выражение Продифференцировав выражение (5.59), имеем Преобразуем выражение (5.61). С этой целью рассмотрим более подробно выражение Второе слагаемое выражения (5.61) представляет собой вектор Но векторный треугольник, изображенный в правой части рис.1.,показывает что в скобке стоит алгебраическая сумма векторов Подставив полученное выражение (5.64) в выражение (5.61) ,имеем следующее равенство  Выражения (5.59) и (5.65) приведены в [3] и [15] и они являются уравнениями связи измеренных и определяемых величин. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 569. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
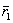 и
и 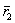 ,а мгновенные скорости –
,а мгновенные скорости – 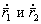 . Остальные изображения и обозначения будут объяснены ниже.
. Остальные изображения и обозначения будут объяснены ниже.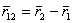 . (5.57)
. (5.57)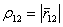 . (5.58)
. (5.58)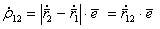 (5.59)
(5.59)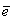 – единичный радиус–вектор изображенный на рис.1 и определяемый по формуле
– единичный радиус–вектор изображенный на рис.1 и определяемый по формуле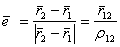 . (5.60)
. (5.60)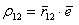 , получаем следующее выражение
, получаем следующее выражение 
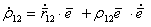 .Но последнее слагаемое равно нулю, так как производная по любой переменной от единичного радиуса–вектора будет производить только его вращения, не меняя модуля (он всегда равен 1), а поэтому все производные будут лежать в касательных плоскостях к сфере единичного радиуса и, следовательно, все будут перпендикулярны к
.Но последнее слагаемое равно нулю, так как производная по любой переменной от единичного радиуса–вектора будет производить только его вращения, не меняя модуля (он всегда равен 1), а поэтому все производные будут лежать в касательных плоскостях к сфере единичного радиуса и, следовательно, все будут перпендикулярны к 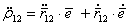 . (5.61)
. (5.61) . Используя (5.60) и продифференцировав его по t ,получим его явное выражение в следующем виде [1]:
. Используя (5.60) и продифференцировав его по t ,получим его явное выражение в следующем виде [1]: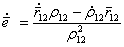 . (5.62)
. (5.62)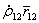 . Но
. Но 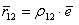 , поэтому второе слагаемое можно представить в следующем виде
, поэтому второе слагаемое можно представить в следующем виде 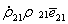 . С учетом вышесказанного, выражение (5.62) принимает следующий вид
. С учетом вышесказанного, выражение (5.62) принимает следующий вид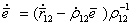 . (5.63)
. (5.63)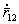 и
и 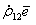 , которые представляют собой некий третий вектор
, которые представляют собой некий третий вектор 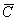 , который изображен так же на рис.1. Согласно [1] , имеем
, который изображен так же на рис.1. Согласно [1] , имеем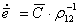 . (5.64)
. (5.64)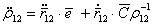 . (5.65)
. (5.65)