
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Явный вид элементов тензора гравитационного поля Земли и его выражение в различных системах координатЗапишем потенциал гравитационного поля Земли в следующем виде где в (5.29) приняты следующие обозначения: m= fM, r0, – средний экваториальный радиус Земли, r, q = 90–j, l – геоцентрические, сферические координаты текущей точки, Plm(cosq) Все три производные первого порядка (5.30)–(5.32) имеют те же обозначения, что и выражение (5.29). В выражении (5.31) введено обозначение Вторые производные будут иметь следующий вид: Кроме того, приведем уравнение Лежандра, связывающее присоединенные функции Лежандра и их первые и вторые производные по x. Имеем а). Выражения тензора геопотенциала в локальной системе координат Введем локальную систему координат начало которой совместим с пробной массой m,имеющей координаты (r, q, l), а ось mx направим по касательной к меридиану из точки m в сторону северного полюса, ось my направим перпендикулярно оси m по касательной к параллели из точки m в сторону Востока, ось mz, дополняя систему до правой, будет направлена в сторону центра масс Земли. В этой системе координат вторые производные будут иметь вид: Выражения вторых производных геопотенциала в локальной системе координат (5.35) являются элементами тензора потенциала притяжения U в локальной системе координат. b).Связь тензоров, выраженных в инструментальной и локальной системах координат  Преобразование элементов любого тензора геопотенциала Т(U) от системы 2 к системе 1 выполняют по известной формуле где П21 есть матрица преобразования системы 2 в систему 1. Введем инструментальную систему, связанную с бортовым градиентометром. Будем полагать, что положение пробных масс с необходимой точностью известно по отношению к центру масс спутника. Поэтому начало инструментальной системы совместим с центром масс спутника m. Ось mxi совместим с вектором скорости спутника Используя свойство скалярного произведения, найдём углы между соответствующими осями локальной и инструментальной системами координат. Угол между осями mxi и myi определяется углом между плоскостью орбиты и плоскостью меридиана, а он находится из скалярного произведения нормалей к этим плоскостям где Из скалярного произведения векторов Угол между осями Из скалярного произведения векторов откуда, аналогично предыдущему, получим Угол между осями Выражение (5.39), выраженное через элементы орбиты, имеет громоздкий вид, поэтому его проще получать по формуле (5.39) в численном виде или получать явную формулу в программной среде МаthCAD или MathLab. Совмещение осей инерциальной системы и локальной проводят в следующем порядке: 1. Вращая по часовой стрелке на угол b вокруг оси mzl, совмещают ось myi с осью myl при помощи матрицы вращения вида 2. Осуществляя поворот на угол g вокруг ранее совмещенных myli, совмещают mzi с mzl матрицей вида 3. Поворотом вокруг оси mz по часовой стрелке на угол 360 – a, совмещают оси mxi и myi при помощи матрицы вращения Преобразование тензора где Таким образом, преобразования элементов матрицы из локальной системы в инструментальную и обратно даются формулами (5.41)–(5.44).
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 845. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
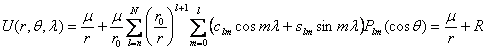 (5.29)
(5.29) – полностью нормированные присоединенные функции Лежандра,
– полностью нормированные присоединенные функции Лежандра, 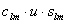 –также полностью нормированные коэффициенты гравитационного поля Земли. Дифференцируя выражения (5.29) в сферической системе координат (r, q, l) легко получить первые производные от возмущающего потенциала R:
–также полностью нормированные коэффициенты гравитационного поля Земли. Дифференцируя выражения (5.29) в сферической системе координат (r, q, l) легко получить первые производные от возмущающего потенциала R: , (5.30)
, (5.30)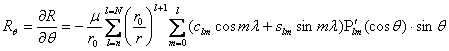 , (5.31)
, (5.31) . (5.32)
. (5.32) , где x=сos
, где x=сos  и при дифференцировании Р, как сложной функции, имеем
и при дифференцировании Р, как сложной функции, имеем 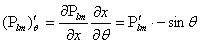 .
. ,
,  ,
, ,
,  ,
,
 . (5.33)
. (5.33) . (5.34)
. (5.34)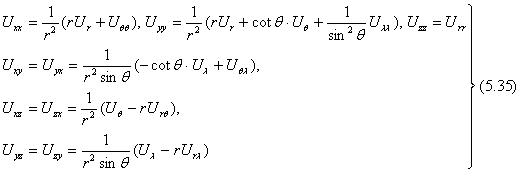
 , (5.36)
, (5.36) , myi совместим с вектором интеграла площадей
, myi совместим с вектором интеграла площадей 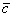 (вектор момента количества движения или, по другой терминологии ,вектор момента скорости), направив его в противоположную сторону вектору
(вектор момента количества движения или, по другой терминологии ,вектор момента скорости), направив его в противоположную сторону вектору  , третья ось mzi, дополняя систему до правой, будет совпадать с вектором, который образуют векторным произведением
, третья ось mzi, дополняя систему до правой, будет совпадать с вектором, который образуют векторным произведением  , где
, где  .
. , (5.37)
, (5.37) – нормаль к орбите и на основании (1) и (3) имеет вид
– нормаль к орбите и на основании (1) и (3) имеет вид  , а
, а 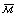 , являющейся нормалью к меридиану, выражается формулой
, являющейся нормалью к меридиану, выражается формулой  .
. .
. и
и 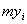 является углом между плоскостями орбиты и параллели, а нормаль к параллели (или касательная к меридиану) имеет вид
является углом между плоскостями орбиты и параллели, а нормаль к параллели (или касательная к меридиану) имеет вид 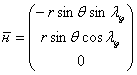 , а вектор
, а вектор  имеем
имеем (5.38)
(5.38) .
.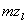 и
и 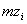 – это угол между радиус–вектором
– это угол между радиус–вектором  и вектором
и вектором  . Угол также находится из скалярного произведения этих векторов аналогично предыдущему
. Угол также находится из скалярного произведения этих векторов аналогично предыдущему . (5.39)
. (5.39)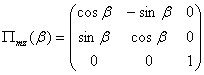 ; (5.40)
; (5.40) ; (5.41)
; (5.41)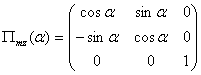
 . (5.42)
. (5.42) будет иметь вид
будет иметь вид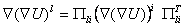 , (5.43)
, (5.43) даются формулами (5.40)–(5.42).Получить матрицу Пil в виде замкнутой формулы возможно в программной среде MathCad или MathLab, но такое выражение не имеет практической ценности в виду его громоздкости. Весьма просто такие операции реализуются в численном виде в вышеуказанных вычислительных средах. Обратные зависимости получают из выражения
даются формулами (5.40)–(5.42).Получить матрицу Пil в виде замкнутой формулы возможно в программной среде MathCad или MathLab, но такое выражение не имеет практической ценности в виду его громоздкости. Весьма просто такие операции реализуются в численном виде в вышеуказанных вычислительных средах. Обратные зависимости получают из выражения . (5.44)
. (5.44)