
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линеаризация уравнений связиПредположим, что мы измеряли взаимные скорости Кроме того, на эти же моменты времени вычислены взаимные скорости Обозначив Аналогично и для относительных ускорений получим следующее выражение Запишем выражение (5.67) без вектора Исходные уравнения оправок для скорости (относительно друг друга) имеют вид а уравнения поправок для ускорений где Проверим, приведенные в [3], выражения (5.70)–(5.71). Исходные уравнения для поправок взаимных скоростей. Из (5.66)–(5.67) имеем Рассмотрим выражение Помножим обе части векторного равенства скалярно на Но второе слагаемое равно 0,так как оно представляет скалярное произведение двух взаимно перпендикулярных векторов по причине, о которой было сказано выше. Поэтому имеем Возвращаясь к выражению (5.73), которое с учетом (5.74) можно переписать После несложных преобразований, выражение (5.75) приобретает вид  Из выражения Подставив в (25.77) во второе слагаемое в скобках выражения (5.75) и заменив вектор Выражение (5.78) служит исходным для составления уравнения поправок. Исходные уравнения поправок для взаимных ускорений Второе уравнение, для получения поправок с использованием ускорений и уравнения (5.71), принимает вид Для формирования коэффициентов в исходных уравнениях поправок продифференцируем каждое слагаемое выражения (5.79) отдельно: первое слагаемое второе слагаемое третье слагаемое Теперь, объединив коэффициенты в уравнении (5.79) при одинаковых производных, можно его представить в виде: Учитывая, что квадрат вектора скорости можно записать в виде Тогда уравнение (5.83) принимает окончательный вид: Выражение (5.86) и является исходным для составления уравнения поправок для ускорений. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 610. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
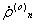 ускорения
ускорения 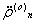 на моменты
на моменты 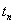 (на самом деле мы их вычислили на основании измеренных расстояний
(на самом деле мы их вычислили на основании измеренных расстояний 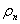 и времени
и времени 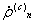 и ускорения
и ускорения 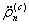 с использованием теории движения ИСЗ и приближенной модели гравитационного поля Земли, т.е.
с использованием теории движения ИСЗ и приближенной модели гравитационного поля Земли, т.е. 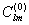 и
и 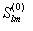 . Взяв между ними разность и разложив в ряд Тейлора, сохранив только линейные члены, мы получим исходные уравнения для поправок. Таким образом, имеем для уравнения (5.59)
. Взяв между ними разность и разложив в ряд Тейлора, сохранив только линейные члены, мы получим исходные уравнения для поправок. Таким образом, имеем для уравнения (5.59)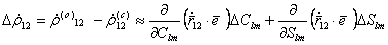 . (5.66)
. (5.66)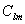 и
и 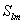 через
через 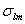 , мы для частной производной по стоксовым постоянным получим следующее выражение
, мы для частной производной по стоксовым постоянным получим следующее выражение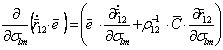 . (5.67)
. (5.67)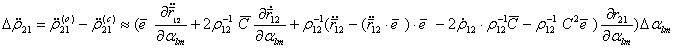 (5.68)
(5.68)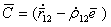 , так как оно будет удобнее при дифференцировании по
, так как оно будет удобнее при дифференцировании по 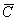 и перемножив скалярно, имеем
и перемножив скалярно, имеем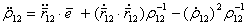 (5.69)
(5.69)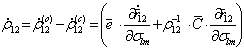 (5.70)
(5.70)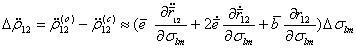 , (5.71)
, (5.71)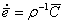 , а
, а 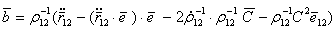 . (5.72)
. (5.72)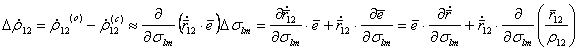
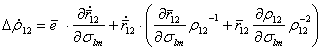 (5.73)
(5.73)
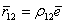 и продифференцируем его по slm. Имеем
и продифференцируем его по slm. Имеем 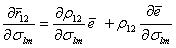 .
.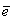 . Получим следующее выражение
. Получим следующее выражение 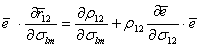 .
.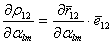 . (5.74)
. (5.74)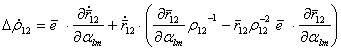 , (5.75)
, (5.75) . (5.76)
. (5.76)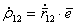 , помножив его скалярно на
, помножив его скалярно на 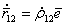 . (5.77)
. (5.77)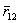 через произведение модуля на единичный вектор, мы получаем в скобках вектор
через произведение модуля на единичный вектор, мы получаем в скобках вектор 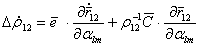 . (5.78)
. (5.78)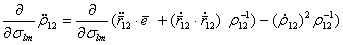 . (5.79)
. (5.79)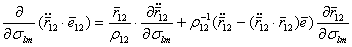 , (5.80)
, (5.80)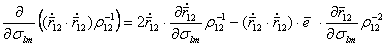 , (5.81)
, (5.81)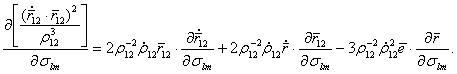 (5.82)
(5.82)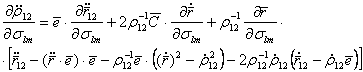 (5.83)
(5.83)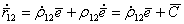 (5.84)
(5.84)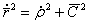 . (5.85)
. (5.85)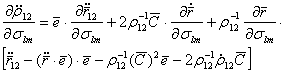 (5.86)
(5.86)