
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Преобразование разности уравнений движения спутников по отношению друг к другуИз векторного треугольника m1m2O, где O центр масс Земли (на рис. 5.2 не отображен) имеем В уравнении движения (5.46) Подставляя (5.48) в уравнение движения (5.46), произведя сокращение и ограничившись линейными членами, получим Используя правила применения оператора Ñ к скалярному произведению векторных величин Ñ и Рассмотрим каждое из четырех полученных слагаемых (5.50). Первое слагаемое имеет в матричной форме следующий вид: Принимая во внимание, что Третье и четвертое слагаемые равны нулю, так как потенциал является безвихревым полем и следовательно, ротор такого поля всегда равен 0 (см.гл.1,п.1.2.7.). Таким образом, с учетом выражений (5.51),(5.52) и вышесказанных замечаний разность уравнений движения для двух спутников преобразуется к виду Выражение Это и есть уравнения описывающее движение спутника m2 относительно спутника m1. В координатной форме можно записать: Уравнения (5.53)–(5.55) аналогичны классическим уравнениям движения, но с той разницей, что в правых частях стоят вторые производные от U, а не первые, как в классических уравнениях. В заключение отметим следующие уравнения (5.53)–(5.55) являются приближенными уравнениями, т.к. во–первых, в разложении (5.48) мы ограничились линейными членами, а во–вторых, расстояние Dr (более 100км.), что составляет только 10–2от расстояния до центра масс Земли.  Поэтому уравнения (5.53–5.55) можно использовать только для приближенных, априорных оценок. Возможно, в этом случае понадобится учет и вторых разностей. Запишем их отдельно от уравнений (5.53)–(5.55), а именно, проделав ту же операцию, что и с линейными членами и следуя правилу применения оператора Ñ к скалярному произведению, имеем: Как следует из (5.41) имеем дело с тензором третьего ранга от гравитационного поля Земли, т.е. третьими производными от геопотенциала. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 633. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
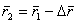 (5.47)
(5.47)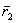 заменим на основании (5.47) и разложим скалярную функцию
заменим на основании (5.47) и разложим скалярную функцию 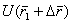 от векторного аргумента
от векторного аргумента 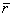 в точке m1 в ряд Тейлора. Имеем следующее выражение
в точке m1 в ряд Тейлора. Имеем следующее выражение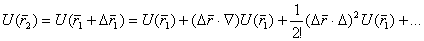 (5.48)
(5.48)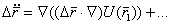 (5.49)
(5.49)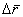 выражения (5.49), получим следующее выражение
выражения (5.49), получим следующее выражение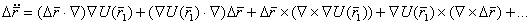 (5.50)
(5.50)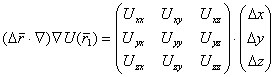 (5.51)
(5.51)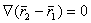 , второе слагаемое в матричной форме запишется так:
, второе слагаемое в матричной форме запишется так: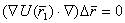 , (5.52)
, (5.52)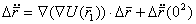 (5.53)
(5.53)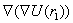 есть градиент силы тяжести в точке m1 и это выражение является тензором гравитационного поля Земли. В матричной форме выражение (5.53) будет иметь следующий вид:
есть градиент силы тяжести в точке m1 и это выражение является тензором гравитационного поля Земли. В матричной форме выражение (5.53) будет иметь следующий вид: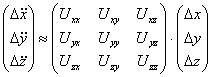 (5.54)
(5.54)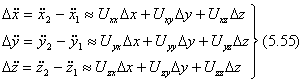
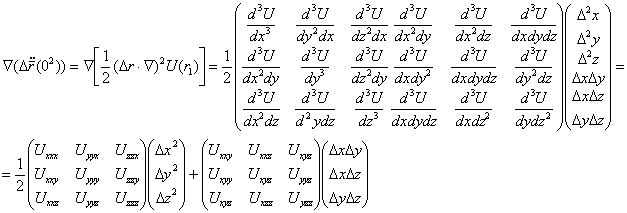 (5.56)
(5.56)