
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Общие свойства непрерывных функций⇐ ПредыдущаяСтр 27 из 27 Теоремы, отражающие основные свойства непрерывных функций, имеют очень простой геометрический смысл. Утверждения теорем легко установить с учетом того, что график непрерывной на промежутке Р функции представляет собой непрерывную (сплошную) кривую на этом промежутке. Поэтому ниже мы приведем лишь формулировки этих теорем. Теорема 1 (вторая теорема Коши). Пусть функция f (x) определена и непрерывна в некотором промежутке Р. Если в двух точках х = х1 и х = х2 (х1 < х2) этого промежутка функция принимает неравные значения f (x1) = у1 и f (x2) = у2, то, каково бы ни было число у3, лежащее между у1 и у2, найдется такая точка х = х3 между х1 и х2, что f (x3) = у3. Следствия: а) значения, принимаемые непрерывной функцией f (x), когда х изменяется в каком-либо промежутке Р,сами также заполняют сплошь некоторый промежуток Е; б) если значения f (x1) и f (x2) разных знаков, то между х1 и х2 необходимо найдется точка х3, в которой функция обращается в нуль: f (x3) = 0 (первая теорема Коши, теорема о корне); в) если функция f (x) непрерывна в точке х = х0 и значение f (x0) отлично от нуля, то для всех достаточно близких к х0 значений х функция f (x) сохраняет тот же знак, какой она имеет в точке х0. Теорема 2. Пусть функция у = f (x) определена, строго монотонно возрастает (убывает) и непрерывна в некотором промежутке Е. Тогда в соответствующем промежутке Е значений этой функции, существует обратная функция х = g (y), также монотонно возрастающая (убывающая) и непрерывная. Теорема 3.Если функция f (x) определена и непрерывна в замкнутом промежутке Р = [a,b], то: а) она ограничена (первая теорема Вейерштрасса) б) достигает в этом промежутке своих точных верхней и нижних границ, (вторая теорема Вейерштрасса).  Иными словами, в промежутке [a,b] найдутся такие точки х = х1 и х = х2, что значения f (х1) и f (х2) будут, соответственно, наибольшим и наименьшимиз всех значений функции f (x). УПРАЖНЕНИЯ 1. На языке « e а) f (x) = ах + b, х0 = 3; б) f (x) = х3, х0 = 2.
2. На языке «последовательностей» доказать, что функция
не является непрерывной в точке х0 = 1. Установить характер разрыва.
3. Доказать непрерывность функции
во всех точках, в которых она определена.
4. Исследовать следующие функции на непрерывность, найти точки разрыва и определить их характер, в случае устранимого разрыва доопределить функцию до непрерывности: а) д) |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 458. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 » доказать непрерывность указанных функций в точке х0.
» доказать непрерывность указанных функций в точке х0.
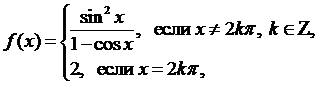
 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; е)
; е)  ; ж)
; ж) 