
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Примеры на нахождение пределов для некоторых неопределенных выражений
1. Пусть функция f (х) = α0 + α1х + . . . + αnхnесть многочлен. Применяя утверждения 8 и 9 (§6, п.6.3), а также результаты примера §6, п.6.1, получим Если х0 является бесконечно удаленной предельной точкой, то
как произведение бесконечно большой величины на ограниченную величину (в круглых скобках все слагаемые, кроме αn ¹ 0, при х ® ∞ бесконечно малые). 2. Пусть функция
Если х0 есть корень знаменателя, но не является корнем числителя, то Если же х0 является корнем и числителя, и знаменателя, то имеет место особый случай, обозначаемый как В этом случае многочлены числителя и знаменателя, согласно теоремы Безу (книга 2, гл. 3, §4), делятся на х – х0 без остатка и следовательно их можно представить в виде
Отсюда, сократив числитель и знаменатель на общий множитель х – х0 получаем
В зависимости от кратности корня х0 эту операцию повторяем до тех пор пока х0 не будет одновременно корнем и числителя, и знаменателя, и тем самым мы не придем к одному из случаев рассмотренных выше. Теперь найдем предел дробно-рациональной функции при условии, что х ® ∞. Рассмотрим следующие случаи. а) Пусть n > m. Тогда, разделив числитель и знаменатель на xm, находим Если теперь перейти к пределу в каждом слагаемом числителя и знаменателя, то в числителе получим бесконечность, а в знаменателе – число bm, т.е. б) Пусть п = т. Тогда, после деления числителя и знаменателя на хт = хп, получаем 
в) Пусть n < m. Тогда, после деления числителя и знаменателя на xn, получаем:
поскольку an есть конечное число, отличное от нуля, а в знаменателе бесконечно большая величина. Таким образом,
3. Вычисление предела для иррациональных функций в особых случаях, характеризуемых символами а) умножения функции f (x) на такую функцию y (x), которая позволяет устранить неопределенность и предел которой равен единице. Например, вычислить предел функции
б) использования формул:
Например, вычислить
4. При вычислении предела неопределенных выражений, содержащих тригонометрические функции, руководствуются, в основном, следующими соображениями и формулами: а) функции
б) функция При в) г) если Например, вычислить
Теперь с учетом в) и г) получаем
5. Нахождение предела неопределенных степенно-показательных выражений, а также выражений, в которые входят показательные и логарифмические функции, в некоторых случаях удается провести при помощи следующих формул:
Например, вычислить Преобразуем функцию, разделив числитель и знаменатель на х – 5. Получим
Теперь с учетом вышеприведенных формул, находим
§7. КЛАССИФИКАЦИЯ БЕСКОНЕЧНО МАЛЫХ И БЕСКОНЕЧНО БОЛЬШИХ ФУНКЦИЙ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО Сравнение бесконечно малых Пусть функции f (x) и y (x) определены и не равны нулю в некоторой окрестности точки х0. Кроме того, при х ® х0 они являются бесконечно малыми, т.е. Во многих случаях представляет интерес сравнение названых бесконечно малых между собой по характеру их приближения к нулю. В основу сравнения двух бесконечно малых f (x) и y (x) кладется поведение их отношения. Если Для сравнимых бесконечно малых функций устанавливаются следующие два соглашения: 1. Если отношение
2. Если же отношение Например, если y (x) = х (х0 = 0), то по сравнению с этой бесконечно малой одного порядка с нею будут и бесконечно малые
Наоборот, бесконечно малые
будут, очевидно, высшего порядка, чем х. Заметим, что если бесконечно малая f (x) оказывается высшего порядка, чем бесконечно малая y (x), то этот факт записывают так: Для более точной сравнительной характеристики поведения бесконечно малых вводят шкалу сравнения бесконечно малых функций, обеспечивающей выражение порядков их – числами. Определение 1.Уславливаются считать бесконечно малую функцию f (x) бесконечно малой к-го порядка малости относительно бесконечно малой функции y (x) при х®х0, если f (x) и Теперь, например, можно, не довольствуясь утверждением, что бесконечно малые (1.22) (при х ® 0) будут бесконечно малыми высшего порядка малости, чем y (x) = х, сказать точно, что первые две из них суть бесконечно малые второго порядка, а последняя – третьего порядка малости относительно y (x) = х, ибо
Остановимся теперь на одном особенно важном частном случае бесконечно малых одного порядка. Определение 2. Две бесконечно малые функции f (x) и y (x) при х ® х0 называются эквивалентными, если их разность g (x) = f (x) – y (x) оказывается бесконечно малой функцией более высокого порядка малости, нежели они сами. Установим полезный критерий эквивалентности двух бесконечно малых, который, в сущности, дает второе определение этого понятия, равносильное данному ранее: Для того, чтобы две бесконечно малые функции f (x) и y (x) были эквивалентны, необходимо и достаточно, чтобы предел их отношения при х®х0 был равен единице, т.е. Эквивалентность функций f(x) и y (x) при х® х0 обозначают f(x) ~ y (x). Основные свойства эквивалентности бесконечно малых функций сводятся к следующим: 1. 2. Если 3. Если 4. При достаточно малых значениях Так, например, при раскрытии неопределенности вида
Примеры. 1. Найти
2. Найти При
|
||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 513. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 ∞
∞ дробно-рациональная. Тогда, используя результаты примера, приведенного выше и утверждение 10 (§6, п.6.3), предполагая, что х0 не есть корень знаменателя, получим
дробно-рациональная. Тогда, используя результаты примера, приведенного выше и утверждение 10 (§6, п.6.3), предполагая, что х0 не есть корень знаменателя, получим
 ∞, как отношение ограниченной величины, отличной от нуля, на бесконечно малую.
∞, как отношение ограниченной величины, отличной от нуля, на бесконечно малую. .
.

 .
.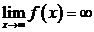 .
. .
. ,
, .
.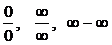 выполняется, в основном, при помощи:
выполняется, в основном, при помощи: при х ® ¥. Умножим функцию f (x) на функцию
при х ® ¥. Умножим функцию f (x) на функцию  , предел которой при х ® ¥ равен единице. Тогда
, предел которой при х ® ¥ равен единице. Тогда
 (1.20)
(1.20) . (1.21)
. (1.21)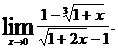 Разделим числитель и знаменатель на х и с использованием (1.20) находим
Разделим числитель и знаменатель на х и с использованием (1.20) находим

 и
и  при стремлении х к ∞ ограничены и предела не имеют. На основание этого
при стремлении х к ∞ ограничены и предела не имеют. На основание этого
 при стремлении х к
при стремлении х к 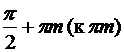 , m = 0, ±1, ±2... бесконечно большая, т.е.
, m = 0, ±1, ±2... бесконечно большая, т.е. 
 .
. ∞, хотя функции
∞, хотя функции  неограниченны, однако предела они не имеют и не являются бесконечно большими. Действительно для этих функций нельзя подобрать такое число dm > 0, чтобы неравенство |f(х)| > m выполнялось бы для всех х > dm ;
неограниченны, однако предела они не имеют и не являются бесконечно большими. Действительно для этих функций нельзя подобрать такое число dm > 0, чтобы неравенство |f(х)| > m выполнялось бы для всех х > dm ; и
и 
 и
и  при
при  то
то 
 Сначала преобразуем функцию
Сначала преобразуем функцию .
. .
.







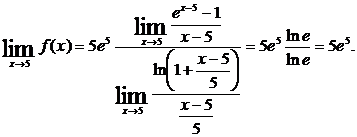
 .
. существует, то бесконечно малые f (x) и y (x) называются сравнимыми, если же этот предел не существует, то бесконечно малые f (x) и y (x) называются несравнимыми. Например, если взять y (x) = х и
существует, то бесконечно малые f (x) и y (x) называются сравнимыми, если же этот предел не существует, то бесконечно малые f (x) и y (x) называются несравнимыми. Например, если взять y (x) = х и  , то их отношение, равное
, то их отношение, равное  при х ® 0 предела не имеет и, следовательно, такие две бесконечно малые несравнимы между собой.
при х ® 0 предела не имеет и, следовательно, такие две бесконечно малые несравнимы между собой. (а с ним и
(а с ним и  ) имеет конечный и отличный от нуля предел при х®х0, то бесконечно малые f (x) и y (x) считаются бесконечно малыми одного порядка малости:
) имеет конечный и отличный от нуля предел при х®х0, то бесконечно малые f (x) и y (x) считаются бесконечно малыми одного порядка малости: .
. стремится к нулю (а отношение
стремится к нулю (а отношение  – к ∞) при х ® х0, то бесконечно малая f (x) считается бесконечно малой высшего порядка малости, чем бесконечно малая y (x), и одновременно бесконечно малая y (x) будет низшегопорядка малости, чем бесконечно малая f (x).
– к ∞) при х ® х0, то бесконечно малая f (x) считается бесконечно малой высшего порядка малости, чем бесконечно малая y (x), и одновременно бесконечно малая y (x) будет низшегопорядка малости, чем бесконечно малая f (x). , ибо, как мы знаем (§6, п.6.4),
, ибо, как мы знаем (§6, п.6.4), .
. (1.22)
(1.22) . Например, можно писать:
. Например, можно писать:  и т.п. Таким образом, символ
и т.п. Таким образом, символ  служит общим обозначением для бесконечно малой высшего порядка, чем y (x).
служит общим обозначением для бесконечно малой высшего порядка, чем y (x). будут бесконечно малыми одного порядка малости, т.е. если
будут бесконечно малыми одного порядка малости, т.е. если  .
. .
. .
.
 то
то 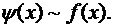
 и
и  то
то 
 и
и  можно со сколь угодно большой относительной точностью положить
можно со сколь угодно большой относительной точностью положить  , т.е. при разыскании предела отношения двух бесконечно малых функций
, т.е. при разыскании предела отношения двух бесконечно малых функций  , при
, при  , каждая из них при этом может быть заменена, без влияния на предел, любой эквивалентной ей бесконечно малой функцией. Действительно, если
, каждая из них при этом может быть заменена, без влияния на предел, любой эквивалентной ей бесконечно малой функцией. Действительно, если  и
и  , т.е.
, т.е.  и
и  , то
, то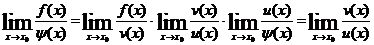 .
. . Поскольку
. Поскольку 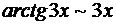 и
и  при
при  , то
, то

 ,
,  Тогда,
Тогда, 