
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Классификация бесконечно больших
Для бесконечно больших функций может быть развита подобная классификация, как и для бесконечно малых. 1. Две бесконечно большие функции f (x) и y (x) при х ® х0 считаются бесконечно большими функциями одного порядка, если их отношение 2. Если же отношение В случае, когда отношение 3. Бесконечно большая функция f (x) называется бесконечно большой k-го порядка относительно бесконечно большой функции y (x) при х®х0 , если f (x) и
УПРАЖНЕНИЯ 1. Найти пределы функций: а) г) ж) к) н) 2. Является ли функция и бесконечно малой если 3. Доказать, что функции а)
НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИИ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО Определение непрерывности функции в точке Функция 1) функция определена в точке х0 и ее окрестности; 2) существует предел функции при х ® х0, который равен значению функции в точке х0.
Равенство (1.23) показывает, что для непрерывных в точке функций знак характеристики функции и знак предела можно менять местами. Здесь  Определение непрерывности функции можно сформулировать в других терминах. Переход от значения х0 к другому значению х можно себе представить так, что значению х0 придано приращение Dх0 = х – х0. Новое значение функции y = f (x) = f (х0+Dх0) разнится от старого у0 = f (x0) на приращение Dу0 = f (х) – f (x0) = f (х0+Dх0) – f (x0). Для того, чтобы функция f (x) была непрерывна в точке х0, необходимо и достаточно, чтобы ее приращение Dу0 в этой точке стремилось к нулю вместе с приращением Dх0 независимой переменной. Иными словами: непрерывная функция характеризуется тем, что бесконечно малому приращению аргумента отвечает бесконечно малое же приращение функции. Возвращаясь к основному определению (1.23), раскроем его содержание на «языке e – Наконец, «на языке последовательностей» (1.13) непрерывность выразится так: какую бы последовательность значений х из окрестности х0: х1,х2,…,хп,…, сходящуюся к х0 , ни взять, соответствующая последовательность значений функции f (х1), f (х2),…, f (хп),… сходится к f (x0). Отметим, что в (1.12) и (1.13) функция f (x) в точке х0 может быть и не определена, но непрерывная в точке х0 функция должна быть определена в этой точке. Поэтому требование |х – х0| > 0 здесь излишне.
Односторонняя непрерывность функции в точке. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 525. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (а с ним и
(а с ним и  ) имеет конечный и отличный от нуля предел при х ® х0.
) имеет конечный и отличный от нуля предел при х ® х0. стремится к ∞ (а обратное отношение
стремится к ∞ (а обратное отношение  – к нулю) при х ® х0, то f (x) считается бесконечно большой функцией высшего порядка, чем y (x), и одновременно, y (x) будет бесконечно большой функцией низшего порядка чем f (x).
– к нулю) при х ® х0, то f (x) считается бесконечно большой функцией высшего порядка, чем y (x), и одновременно, y (x) будет бесконечно большой функцией низшего порядка чем f (x). при х ® х0 ни к какому пределу не стремится, бесконечно большие функции f (x) и y (x) будут несравнимы.
при х ® х0 ни к какому пределу не стремится, бесконечно большие функции f (x) и y (x) будут несравнимы. будут бесконечно большими при х ® х0 одного порядка, т.е. если
будут бесконечно большими при х ® х0 одного порядка, т.е. если
 ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  ;
; ; з)
; з)  ; и)
; и)  ;
; ; л)
; л)  ; м)
; м)  ;
; ; о)
; о)  .
.  бесконечно большой, если
бесконечно большой, если 
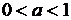 при
при  ?
? есть бесконечно большими:
есть бесконечно большими:
 называется непрерывной в некоторой точке х0, если:
называется непрерывной в некоторой точке х0, если: . (1.23)
. (1.23) .
. » (1.12). Смысл непрерывности функции f (x) в точке х0 сводится к следующему: каково бы ни было число
» (1.12). Смысл непрерывности функции f (x) в точке х0 сводится к следующему: каково бы ни было число  , для него найдется такое число
, для него найдется такое число  , что неравенство
, что неравенство  влечет за собой
влечет за собой  . Последнее неравенство, таким образом, должно выполняться в достаточно малой окрестности
. Последнее неравенство, таким образом, должно выполняться в достаточно малой окрестности  точки х0.
точки х0.