
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Функции, непрерывные в промежуткеФункция f (x) называется непрерывной слева от точки х0, если: 1) функция определена в точке х0 и в левой ее полуокрестности; 2) существует предел функции в точке х0 слева и этот предел равен значению функции в этой точке:
Аналогично определяется непрерывность функции справа от точки х0. Условие 2) при этом запишется в виде:
Если жех0есть внутренняя точка промежутка, т.е. функция f (x) определена как слева, так и справа от точки х0, то для того, чтобы выполнялось равенство (1.23), выражающее непрерывность функции в точке х0 в обычном смысле, необходимо и достаточно, чтобы имели место оба равенства одновременно: и (1.24), и (1.25). Иными словами, непрерывность функции в точке х0 равносильна ее непрерывности в этой точке одновременно справа и слева. Если функция непрерывна в каждой внутренней точке х интервала (a,b), то такая функция называется непрерывной в интервале(a,b). Если функция непрерывна в каждой внутренней точке х сегмента [a,b], а в концевых точках – для левого конца непрерывна справа, а для правого конца непрерывна слева, т.е.
то говорят, что функция у = f(x) непрерывна на сегменте [a,b]. График функции, непрерывной в промежутке, представляет собой непрерывную (сплошную) линию на этом промежутке.
Равномерная непрерывность Предположим, что функция у = f (x) определена и непрерывна во всем промежутке Р (замкнутом или нет, конечном или бесконечном), т.е. непрерывна в каждой точке х0ÎР. Тогда для каждой точки х0 из Р в отдельности по заданному 
Рис. 14
Таким образом, по отношению к функции f (x), непрерывной в промежутке Р, встает вопрос: существует ли, при заданном e , такое de , которое годилось бы для всех точек х0 из этого промежутка? Определение. Если для каждого числа e > 0 найдется такое число de > 0, что |х–х0| < de влечет за собой |f (x) – f (x0)| < e , где бы в пределах рассматриваемого промежутка Р ни лежали точки х0 и х, то функцию f (x) называют равномерно непрерывной в промежутке Р. В этом случае число de оказывается зависимым только от e и может быть указано до выбора точки х0: de годится для всех х0одновременно. Равномерная непрерывность означает, что во всех частях промежутка достаточна одна и та же степень близости двух значений аргумента х1 и х2, чтобы добиться заданной степени близости соответствующих значений функции f (x1) и f (x2), т.е. для любого e > 0 можно найти de > 0, зависящее только от e , такое, что х1и х2 из промежутка Р, удовлетворяющих неравенству |х2 – х1| < de , значения функции удовлетворяют неравенству |f (x2) – f (x1)| < e . Непрерывность функции во всех точках промежутка не влечет необходимо за собой ее равномерной непрерывности в этом промежутке. Однако, если этот промежуток Р замкнут, т.е. если Р = [a,b], то справедлива теорема, принадлежащая Кантору и которую мы примем без доказательства. Теорема Кантора. Если функция f (x) определена и непрерывна в замкнутом промежутке [a,b], то она и равномерно непрерывна в этом промежутке.
8.4. Разрывы функции. Классификация разрывов
Если функция определена в некоторой окрестности точки х0 и, может быть, в самой точке х0, однако условия непрерывности в этой точке не выполняются, то точка х0 называется точкойразрыва функции, а функция называется разрывной. Остановимся подробнее на вопросе о разрыве функции f (x) в точке х0 и рассмотрим три случая. 1. Функция определена в точке х0 и ее окрестности. Для нее в точке х0 существуют конечные односторонние пределы. Тогда точка х0 будет точкой разрыва функции если: а) б) в) или Такие разрывы функции называют обыкновенным или разрывом первого рода. В этом случае говорят также, что функция f (x) в точке х0 производит скачок, по величине равный f (x + 0) – f (x0 – 0). Если в точке х0 скачок функции равен нулю, т.е.
Таким образом, точки разрыва первого рода делятся на точки устранимого и точки неустранимого разрыва. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 674. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . (1.24)
. (1.24) (1.25)
(1.25) и
и  ,
,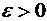 найдется
найдется  , что
, что  влечет за собой
влечет за собой  . При изменении х0 в пределах Р,даже если
. При изменении х0 в пределах Р,даже если  неизменно, число de , вообще говоря, будет меняться. В достоверности этого можно убедиться из рисунка 14. Число de , пригодное на участке, где функция изменяется медленно (график представляет пологую кривую), может оказаться слишком большим для участка быстрого изменения функции (где график круто поднимается или опускается). Иными словами, число de вообще зависит не только от e , но и от х0.
неизменно, число de , вообще говоря, будет меняться. В достоверности этого можно убедиться из рисунка 14. Число de , пригодное на участке, где функция изменяется медленно (график представляет пологую кривую), может оказаться слишком большим для участка быстрого изменения функции (где график круто поднимается или опускается). Иными словами, число de вообще зависит не только от e , но и от х0.
 – функция f(x) имеет в точке х0 разрыв справа;
– функция f(x) имеет в точке х0 разрыв справа; – разрыв слева;
– разрыв слева;
 – функция f (x) имеет в точке х0 разрывы как справа, так и слева.
– функция f (x) имеет в точке х0 разрывы как справа, так и слева. , то точка х0 называется точкой устранимого разрыва. В случае устранимого разрыва функцию можно доопределить так, чтобы получить непрерывную функцию в этой точке. Например, функцию
, то точка х0 называется точкой устранимого разрыва. В случае устранимого разрыва функцию можно доопределить так, чтобы получить непрерывную функцию в этой точке. Например, функцию  , для которой, как
, для которой, как 
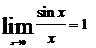 (или
(или 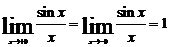 ) можно доопределить и получить непрерывную функцию
) можно доопределить и получить непрерывную функцию