
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Арифметические операции над непрерывными функциямиТеорема. Если две функции f (x) и g (x) определены в одном и том же промежутке Р и обе непрерывны в точке х0, то в этой же точке будут непрерывны и функции f (x) ± g (x), f (x)·g (x), Это непосредственно вытекает из теорем о пределе суммы (разности), произведения и частного двух функций, имеющих порознь пределы (гл.1, §6, п.6.3). Остановимся для примера на частном двух функций. Предположение о непрерывности функций f (x) и g (x) в точке х0 равносильно наличию равенств
Но отсюда, по теореме о пределе частного (так как предел знаменателя не нуль), имеем:
а это равенство и означает, что функция Следствия. 1. Линейная комбинация непрерывных функций есть функция непрерывная. 2. Произведение конечного числа непрерывных функций есть функция непрерывная. 3. Если f (x) непрерывна, то непрерывна и |f (x)|. В качестве иллюстрации приложения данной теоремы рассмотрим непрерывность целой и дробной рациональных функций. Функция f (x) = х, очевидно, непрерывна на всем промежутке (-¥,+¥): если хп ® х0, то f (xп) = хп ® х0 = f (x0). Точно так же непрерывна и функция, сводящаяся тождественно к постоянной. Отсюда, на основании вышеприведенной теоремы, вытекает уже непрерывность любого одночленного выражения Очевидно, наконец, что и частное двух полиномов (дробно-рациональная функция):
также будет непрерывно при каждом значении х, кроме тех, которые обращают знаменатель в нуль. Таких точек непременно конечное число, поскольку число корней целой рациональной функции не более наивысшего показателя степени многочлена, стоящего в знаменателе. Причем, это точки разрыва второго рода. 
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 578. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
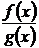 , последняя при условии, что g(x) ¹ 0.
, последняя при условии, что g(x) ¹ 0.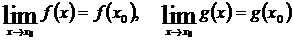 .
. ,
,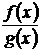 непрерывна в точке х0.
непрерывна в точке х0. как произведения непрерывных функций, а затем и полинома (целой рациональной функции)
как произведения непрерывных функций, а затем и полинома (целой рациональной функции) 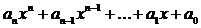 как суммы непрерывных функций. Во всех упомянутых случаях непрерывность имеет место во всем промежутке (-∞,+∞).
как суммы непрерывных функций. Во всех упомянутых случаях непрерывность имеет место во всем промежутке (-∞,+∞).