
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Непрерывность и разрывы монотонной функцииРассмотрим функцию f (x), которая, – при изменении х в промежутке Р – монотонно возрастает (убывает) хотя бы в широком смысле (гл.1, §4, п.4.4). По отношению к таким функциям имеет место следующая теорема. Теорема 1. Монотонно убывающая (возрастающая) функция f(x) может иметь в Р разве лишь разрывы первого рода, т.е. скачки. Возьмем любую точку х0 промежутка Р, и пусть она не является левым концом этого промежутка. Рассматривая ту часть промежутка, которая лежит влево от х0, применим к ней теорему 12 из §6, п.6.3 о пределе монотонной функции: поскольку для х < х0, очевидно, f (x) ≤ f (x0), то существует конечный предел Если он совпадает со значением f (x0), то слева в точке х0 функция непрерывна; в противном случае – налицо скачок. Аналогично убеждаемся в том, что в каждой точке х0 промежутка Р (не служащей правым его концом) справа тоже либо имеет место непрерывность, либо скачок. С помощью доказанной теоремы легко установить критерий непрерывности монотонной функции. Теорема 2. Если значения монотонно возрастающей (убывающей) в промежутке Р функции f (x) содержатся в промежутке Е и сплошь заполняют его (так что каждое значение у из Е принимается функцией хоть раз), то эта функция непрерывна в Р. Допустим, что в какой-нибудь точке х0 из Р функция f (x) имеет разрыв, например, слева; как мы видели, этот разрыв может быть только скачком. В этом случае существует предел f (x0 – 0), но он меньше значения f (x0). Так как для 
Непрерывность сложной функции Теорема. Пусть функция j (у) определена в промежутке Е, а функция f (х) – в промежутке Р, причем значения последней функции не выходят за пределы Е, когда х изменяется в Р. Если f (х) непрерывна в точке х0 из Р, а j (у) непрерывна в соответствующей точке у0 = f (х0) из Е, то и сложная функция j [f (х)] будет непрерывна в точке х0. Доказательство. Зададимся произвольным числом |j (у) – j (у0)| < С другой стороны, ввиду непрерывности f (x) при х = х0, по d найдется такое s > 0, что из |х – х0| < s следует |f (x) – f (x0)| = | у –у0| < d . По самому выбору числа d отсюда следует далее
Этим "на языке
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 608. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. будет
будет  а для
а для  очевидно,
очевидно,  то функция не может принимать значений у, лежащих между числами
то функция не может принимать значений у, лежащих между числами  и f (x0), принадлежащих промежутку Е. Это противоречит условию теоремы; значит, функция
и f (x0), принадлежащих промежутку Е. Это противоречит условию теоремы; значит, функция  разрывов не имеет.
разрывов не имеет.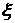 > 0. Так как j (у) непрерывна при у = у0, то по
> 0. Так как j (у) непрерывна при у = у0, то по  найдется такое d > 0, что из |у – у0| < d следует
найдется такое d > 0, что из |у – у0| < d следует .
. " и доказана непрерывность функции
" и доказана непрерывность функции  в точке х0.
в точке х0.