
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение и геометрическое истолкование предела функцииПусть f – числовая функция переменного х, определенная на числовом множестве P, для которого х0 является точкой сгущения. Нас будет интересовать, как ведут себя значения y = f(x) функции f, когда аргумент х стремится к х0. Определение 1(предел функции по Коши). Постоянное число l называют пределом функции f переменного х при стремлении х к х0 (или в точке х0), если для каждого
где х взято из области определения Р функции f и отлично от точки сгущения х0 множества Р. Определение 2(предел функции по Гейне).Постоянное число l называют пределом функции f переменного х, если для любой последовательности значений аргумента х1,х2,…,хп,… из области определения P функции f, имеющей пределом число х0 Эти два определения предела функции равносильны. Тот факт, что l является пределом функции f(x) при х ® х0, записывают так:
Геометрическое определение предела функции можно истолковать следующим образом. Число l является пределом функции f(x) при х ® х0, если для любой
Рис. 13
На рис.13 сплошной кривой показаны точки графика функции f(x), для которых координата  Пример. Доказать, что Преобразуем неравенство
Допустим, что функция f(x) определена в некоторой окрестности точки 2, например, (0,4). С учетом этого
Таким образом, если положить
6.2. Односторонние и бесконечные пределы функции
Если область определения Р функции f(x) такова, что в любой близости от х0, но справа от х0, найдутся отличные от х0 значения х из Р (в этом случае точку х0 называют правой точкой сгущения для Р), то можно специализировать только что данные определения предела функции, ограничившись лишь значениями Аналогично устанавливается понятие о левой точке сгущения и о пределе функции при стремлении х к х0 слева или о пределе (в точке х0) слева: Если точка х0 является одновременно точкой сгущения для Р и правой, и левой, то, как легко установить, для существования предела (1.13) необходимо и достаточно существование порознь и равенство пределов справа и слева:
Когда х0 = 0, вместо 0 + 0 (0 – 0) пишут +0 (–0). При стремлении х к конечному пределу х0 функция может иметь и бесконечный предел (без знака или определенного знака). Определение 1.Функция f(x) имеет пределом ¥ при стремлении х к х0 (в точке х0), если для каждого числа m > 0 найдется такое число dm > 0, зависящее от m, что
(где, как и всегда, х взято из Р и отлично от х0). Если при этом функция f(x) для достаточно близких к х0 значений х сохраняет положительный (отрицательный) знак, так что первое из неравенств (1.15) может быть заменено более узким: f(x) > m (f(x) < m), то говорят о пределе +∞ (–∞). Запись этих фактов аналогична (1.13): Для рассмотренного случая могут быть повторены сделанные выше замечания относительно односторонних пределов справа и слева. Если множество Р содержит сколь угодно большие (по абсолютной величине) значения х (множество Р неограниченно), то говорят, что ¥ является точкой сгущения для Р. В этом предположении дадим следующее определение. Определение 2. Функция f(x) при стремлении х к ∞ имеет предел l, если, каково бы ни было число
(где х берется из Р). При этом пишут: Если рассматриваются лишь положительные (или лишь отрицательные) значения х, то говорят о пределе функции при стремлении х к +¥ (или к –¥). Наконец, легко перефразировать все сказанное на случай l = ¥, +¥ или –¥. При стремлении функции f(x) к нулю ее называют бесконечно малой; ее называют бесконечно большой, если f(x) стремится к ¥. Если последнее обстоятельство имеет место при х ® х0, то говорят также, что в точке х0 функция обращается в бесконечность. Пример 1. Рассмотрим функцию
Очевидно, Отсюда, на основании (1.14), можно заключить, что Пример 2. Докажем, что При любом m > 0 достаточно взять dm = loga m, чтобы х > dm влекло за собой ах > m, что и доказывает наше утверждение. Аналогично доказывается, что Именно, каково бы ни было Если же 0 < а < 1, то с помощью преобразования
Основываясь на этих случаях, можно показать, что Пример 3. Руководствуясь примером 2, легко установить, что: Следовательно, функция Пример 4. Показать, что функция Пусть задано m > 0. Найдем такую dm - окрестность нуля, что при всех х из этой окрестности (х ¹ 0) выполняется неравенство Рассмотрим неравенство
Положив Заметим, что
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 583. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 найдется такое число
найдется такое число 
 , зависящее от
, зависящее от 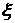 , что
, что  , лишь только
, лишь только (1.12)
(1.12) где х0 может и не принадлежать области Р), последовательность значений функции f(x1), f(x2), …, f(xп), … для этих значений аргумента имеет пределом число l,
где х0 может и не принадлежать области Р), последовательность значений функции f(x1), f(x2), …, f(xп), … для этих значений аргумента имеет пределом число l,  .
. . (1.13)
. (1.13)
 (х0 –d, х0+d), а уÎ(l–
(х0 –d, х0+d), а уÎ(l– 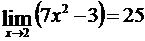 . Пусть задано любое
. Пусть задано любое  . Найдем
. Найдем  такое, что для всех х, удовлетворяющих неравенствам
такое, что для всех х, удовлетворяющих неравенствам  выполняется неравенство
выполняется неравенство 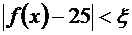 . Условие
. Условие  означает, что х ¹ 2.
означает, что х ¹ 2.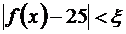 .
. .
. или
или  .
. , тогда для всех
, тогда для всех  , справедливо неравенство
, справедливо неравенство  , а это означает, что
, а это означает, что 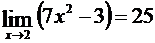 .
. . В этом случае предел функции, если он существует, называется пределом функции f(x) при стремлении х к х0 справа, или, короче, пределом (в точке х0) справа и обозначается символом
. В этом случае предел функции, если он существует, называется пределом функции f(x) при стремлении х к х0 справа, или, короче, пределом (в точке х0) справа и обозначается символом  .
. .
. =
=  = l. (1.14)
= l. (1.14) , лишь только
, лишь только 
 (1.15)
(1.15) .
. , для него существует такое число
, для него существует такое число  , зависящее от
, зависящее от  , что
, что , лишь только
, лишь только 
 .
.
 .
. не существует.
не существует. (при а > 1).
(при а > 1).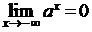 (при а > 1).
(при а > 1). , если взять
, если взять  , то при
, то при  необходимо
необходимо  .
. легко установить результаты
легко установить результаты (при 0 < а < 1).
(при 0 < а < 1). (при а > 0 и а ¹ 1) и, следовательно, функция f(x) = ах при х ® ¥ является бесконечно большой. Однако, если х ® –¥ (при а > 1) и х ® +¥ (при 0 < а < 1), то функция f(x) = ах является бесконечно малой.
(при а > 0 и а ¹ 1) и, следовательно, функция f(x) = ах при х ® ¥ является бесконечно большой. Однако, если х ® –¥ (при а > 1) и х ® +¥ (при 0 < а < 1), то функция f(x) = ах является бесконечно малой. (при а > 1);
(при а > 1);  (при 0 < а < 1);
(при 0 < а < 1);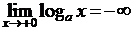 (при а > 1);
(при а > 1);  (при 0 < а < 1).
(при 0 < а < 1). (при а > 0 и а ¹ 1) при х ® +¥ и х ® +0 является бесконечно большой, т.е.
(при а > 0 и а ¹ 1) при х ® +¥ и х ® +0 является бесконечно большой, т.е.  и
и  .
. при х ® 0 является бесконечно большой, т.е.
при х ® 0 является бесконечно большой, т.е.  .
. .
. . Из этого неравенства следует:
. Из этого неравенства следует: .
. , получим, что, как только
, получим, что, как только  , имеем
, имеем  ∞.
∞. ;
;  . Однако несмотря на это условие (1.14) для существования предела в точке х0 = 0 считается выполненным l =∞.
. Однако несмотря на это условие (1.14) для существования предела в точке х0 = 0 считается выполненным l =∞.