
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Принцип сходимости последовательностиЗададимся теперь вопросом об общем признаке существования конечного предела любой последовательности, т.е. отысканием такого условия для сходимости последовательности, которое обладало бы свойством необходимости и достаточности. Поставленную задачу решает теорема Больцано-Коши, которую часто называют также принципом сходимости. Теорема (Больцано-Коши).Для того чтобы последовательность Суть дела здесь в том, чтобы значения последовательности между собой безгранично сближались по мере возрастания их номера. Доказательство теоремы опускаем. УПРАЖНЕНИЯ 1. Доказать, что множество 2. Дана последовательность с общим членом а) Доказать, что б) Будет ли эта последовательность монотонной? в) Найдите sup yn и inf yn. 3. Дана последовательность с общим членом 4. Доказать, что функции y = sin x и y = tg x периодические и определить их периоды. 5. Найдите пределы: а) в) 6. Доказать, что 7. Является ли последовательность 8. При каких условиях параметрические уравнения: а) определяют функцию y = f(x)? Найти явный вид этих функций, а также уравнения F(x, y) = 0, посредством которых эти функции заданы неявно.
ПРЕДЕЛ ЧИСЛОВОЙ ФУНКЦИИ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 650. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 вообще имела конечный предел, необходимо и достаточно, чтобы для каждого
вообще имела конечный предел, необходимо и достаточно, чтобы для каждого  существовал такой номер
существовал такой номер  , чтобы неравенство
, чтобы неравенство  выполнялось лишь только
выполнялось лишь только 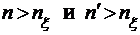 .
. ограничено.
ограничено. .
. ;
; . Пользуясь вторым определением предела, доказать, что
. Пользуясь вторым определением предела, доказать, что  .
. ; б)
; б)  ;
; ; г)
; г) 

 бесконечно большой?
бесконечно большой? ; б)
; б)  ; в)
; в) 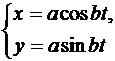 ; г)
; г) 