
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сингулярное разложение матрицТеорема (Cингулярное разложение). Любая матрица где · диагональные элементы σii являются сингулярными числами матрицы A; · столбцы матрицы U образуют ортонормированный базис из собственных векторов матрицы AA∗; · столбцы матрицы V образуют ортонормированный базис из собственных векторов матрицы Доказательство. Согласно свойству 70 знакоопределенных матриц эрмитова матрица A∗A являетсяположительнополуопределённой. Пусть σ21,…, σ2n – собственные значения матрицы По системе векторов v1,…, vnпостроим второй сингулярный базис u1,…, um(если r<m, то систему ортонормированных векторов u1,…, urдобавим до ортонормированного базиса в m-мерном пространстве. Составим из векторов v1,…, vnи u1,…, umдве унитарные матрицы: V ={v1,…, vn}∈
Полярное разложение матриц Теорема (Полярное разложение). Если A∈ Более того, Доказательство. Положим Где U,V – матрицы из сингулярного разложения (1). Несложно проверить, что W – унитарная матрица, а H – положительно полуопределенная эрмитова матрица. Тогда имеем: 
Далее, так как Применяя полученный результат к
Векторные нормы. Непрерывность векторных норм Векторная норма: функция 1) 1а) 2) 3) Векторная полунорма: выполняются 1),2),3),но не обязательно 1а) Определение. Вектор, норма которого равна единице, называется нормированным. Любой ненулевой вектор x можно нормировать, умножив его на число λ=||x||-1 Примеры векторных норм наCn. Евклидова норма(I2, 2-норма) ||x||2=( Абсолютная норма(I1, 1-норма, Манхеттен-норма) ||x||1 Максимальная норма(I∞, ∞-норма)||x||∞ Норма Гёльдерас показателем р(Ip – норма) ||x||p Теорема(о непрерывности нормы) Векторная норма ||•||непрерывно зависит от элементов вектора, т.е. для заданного ε > 0 ∃δ(ε) > 0, такое что | ||x|| - ||y|| | < ε, как только|xi −yi| <δ(ε) для всех индексов i. Доказательство. Пусть x,y∈Cn заданные векторы. Используя единичные векторы ei, можно представить
Определим число k =max||ei||>0. Тогда справедлива цепочка соотношений:
Для заданного ε определим
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 663. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
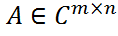 ранга r может быть представлена в виде
ранга r может быть представлена в виде 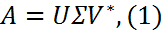
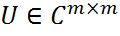 ,
, 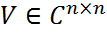 – унитарные матр.,
– унитарные матр., 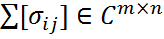 – диагональная прямоугольная матр. с невозрастающими неотрицательными элементами по диагонали. При этом
– диагональная прямоугольная матр. с невозрастающими неотрицательными элементами по диагонали. При этом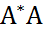 ;
;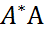 причем σi упорядочены.Пусть v1, . . . ,vn– собственные векторы матрицы
причем σi упорядочены.Пусть v1, . . . ,vn– собственные векторы матрицы  , соответствующие σ21,…, σ2n. Из спектральной теоремы для нормальныхматниц следует, что v1,…, vnможно выбрать ортонормированными.
, соответствующие σ21,…, σ2n. Из спектральной теоремы для нормальныхматниц следует, что v1,…, vnможно выбрать ортонормированными.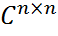 , U ={ и u1,…, um}∈
, U ={ и u1,…, um}∈ 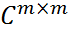 . Составим также диагональную матрицу Σ=diag{σ1, . . . ,σn}. Тогда A=UΣV∗.
. Составим также диагональную матрицу Σ=diag{σ1, . . . ,σn}. Тогда A=UΣV∗.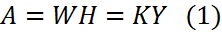
 .
.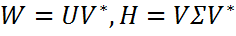 (2),
(2),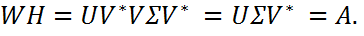
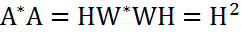 =, то верно и
=, то верно и  .
.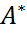 , получим
, получим .
.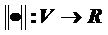 :
: 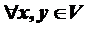
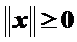 (неотрицательность);
(неотрицательность); (невырожденность);
(невырожденность);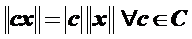 (абсолютная однородность);
(абсолютная однородность);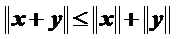 (неравенство треугольника).
(неравенство треугольника).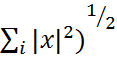
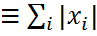
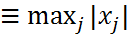


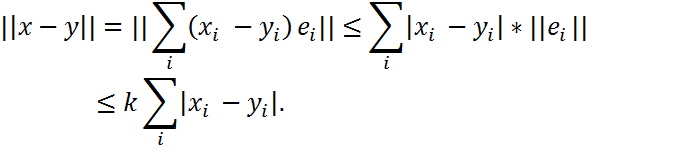
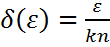 и рассмотрим x и y, для которых |
и рассмотрим x и y, для которых |  | <δ, i=1,n. Тогда
| <δ, i=1,n. Тогда