Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЭквивалентностьвекторныхнормТеорема (об эквивалентности векторных норм). Пусть ||•||α и||•||β–две произвольные векторные нормы в конечномерном вещ. Или комплексном пространствеV. Тогда они эквивалентны. Доказательство. Рассмотрим соотношение Сфера явл. компактным мно-вом в cm≤ h≤ cM откуда следует, что соотношение теоремы верно ∀x∈S. Рассмотрим теперь произвольный вектор x∈V . Случай x = 0 тривиален, поэтому считаем, что x ≠ 0. Очевидно, что y= откуда получаем откуда в силу св-ва 2) векторных норм следует справедливость теоремы для ∀x∈
Матричные нормы Опр. Ф-ция ||•||: 1)||A||≥0(неотрицательность); 1а) A||=0 2)||αA||=|α A|| (абсолютная однородность); 3)||A+B||≤||A||+||B|| (неравенство треугольника); 4)||AB||≤||A B|| (кольцевое свойство) Примеры матричных нормна 1*.||A||1 ≡ Столбцовая норма (1-норма), 2*.||A||∞ ≡ Строчная норма (∞-норма), 3*.||A||E ≡ Евклидова норма 4*.||A||E ≡ Спектральная норма 5*.||A||M ≡ М-норма 6*. ≡ l1-норма Согласованные и подчиненные векторные и матричные нормы. Определение. Матричная норма ||•||M называется согласованнойс векторной нормой ||•||V , если  ||A||V≤ ||A||M ||x||V (1) для любой матрицы A и всех векторов x. Определение. Пусть задана векторная норма ||•||V. Тогда числовая функция
называется нормой матрицы, подчиненной (индуцированной) векторной норме ||•||V. Теорема(Подчиненная векторная норма). Функция (2) определена и является согласованной нормой в Теорема.Для подчиненной матричной нормы справедливо ||Ax||≤||A X||, ||E||=1 Доказательство
Следствие. Матричная норма||•||M, подчиненная векторной норме||•||V, согласована с этой нормой. Матричная норма, подчиненная векторной норме||•||∞ Получим оценку сверху для величины ||Ax||∞ ||Ax||∞ Покажем, что эта оценка достигается. Пусть максимум по i имеет место при i=l. Возьмем x=(sign(al1),…,sing(aln)). Имеем Таким образом,
Число обусловленности. Определение. Величина
называется числом обусловленности матрицы A по отношению к матричной норме ||•||. Свойства числа обусловленности 10. Для любой матричной нормы cond(A)≥1. 20. Для любой матрицы A и любого числа α выполняется равенство cond(A) =cond(αA). 30. Для спектральной и евклидовой норм число обусловленности не меняется при умножении матрицы слева и справа на любую унитарную матрицу. 40. Для 1-, 2-, ∞-норм и евклидовой нормы число обусловленности не меняется при перестановке строк и столбцов. 50. Для спектральной нормы число обусловленности любой матрицы равно отношению максимального сингулярного числа к минимальному.
Сходимость матриц Определение. Матрица А называется сходящейся, если Лемма. Доказательство. ||Ak||≤||A||k→k→0 0 Теорема.Матрица Доказательство .Пусть Ak→0.Рассмотрим собственный вектор x≠0: Ax=λx. Тогда A2x=A(Ax)=A(λx)=λ(Ax)=λ2x…Akx=λkx→0 Обратно Следствие.
Теорема Гершгорина Теорема Гершгорина и ее следствия. Для произвольной матрицы AЄ
Наиболее полезная и легко применяемая теорема, дающая оценка для собственных значений – теоремы Гершгорина. Теорема Гершгорина (строчная).Все собственные значения матрицы A заключены в объединении n кругов
Кроме того, если объединение k из этих кругов есть связная область, не пересекающаяся с остальными n−k кругами, то в ней находится ровно k собственных значений матрицы A. Теорема (Гершгорина (столбцовая)). Все собственные значения матрицы AЄ
Кроме того, если k из этих кругов образуют область, изолированную от остальных n-k кругов, то в ней находится ровно kсобственных значений матрицы А.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 572. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
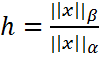 на евклидовой единичной сфере
на евклидовой единичной сфере 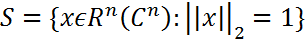
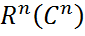 . Так как
. Так как 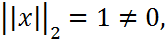 то по св-ву 1а) векторгой нормы
то по св-ву 1а) векторгой нормы 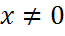 , и, хначит,
, и, хначит, 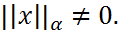 Таким образом, значенатель не образается в нуль и отношение непрерывно на S. По теореме Вейерштрасса у непрерывной ф-цииh на компактноммн-веS сущ. максимальное значение cM и положительное (т.к. h>0) минимальное значение cm:
Таким образом, значенатель не образается в нуль и отношение непрерывно на S. По теореме Вейерштрасса у непрерывной ф-цииh на компактноммн-веS сущ. максимальное значение cM и положительное (т.к. h>0) минимальное значение cm: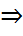 cm ≤
cm ≤ 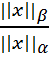 ≤ cM,
≤ cM, ∈S. Тогда по вышеуказанномуcm||y||α≤||y||β≤ cM||y||α,
∈S. Тогда по вышеуказанномуcm||y||α≤||y||β≤ cM||y||α,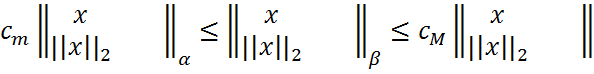 ,
,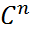
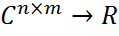 , наз. матричной нормой, если для любой A ∈
, наз. матричной нормой, если для любой A ∈ 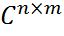 выполняются следующие условия:
выполняются следующие условия: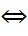 A=0 (невырожденность);
A=0 (невырожденность);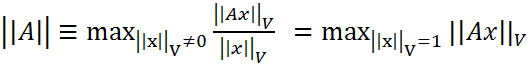 (2)
(2)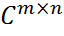 для любых норм в Cm и Cn.
для любых норм в Cm и Cn.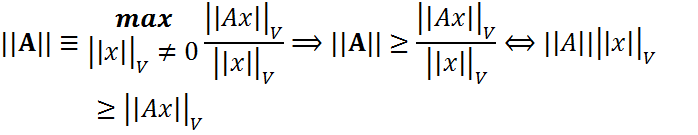
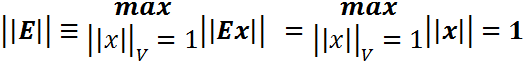
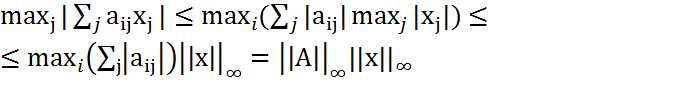 .
.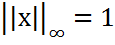 и точные равенства во всей цепочке выше.
и точные равенства во всей цепочке выше.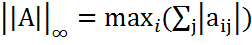 подчиненная векторной норме||•||∞
подчиненная векторной норме||•||∞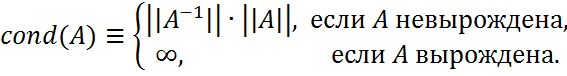 (1)
(1)
 ||•||: ||A||<1
||•||: ||A||<1 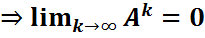 .
. Ak→||•||0
Ak→||•||0 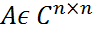 является сходящейся тогда и только тогда, когда
является сходящейся тогда и только тогда, когда 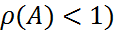 .
.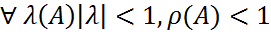 .
.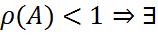 ||
|| 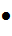 ||:||A||<1
||:||A||<1 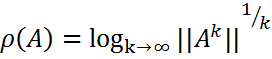
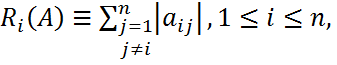 - строчная почти-нормы, а также
- строчная почти-нормы, а также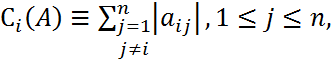 - столбцовые почти – нормы матр. А.
- столбцовые почти – нормы матр. А.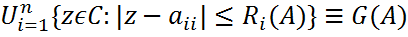
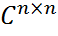 принадлежат объединению nкругов (столбцовой области Гершгорина)
принадлежат объединению nкругов (столбцовой области Гершгорина)