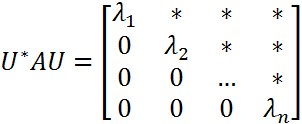Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Критерии унитарности матрицыМатрица U ∈ Cn × n называется унитарной, если U*U = E. Если к тому же U ∈ Rn × n , то U называется ортогональной. Теорема (о критериях унитарности). Следующие предложения эквивал. для матрицы U ∈ Cn × n : a) U унитарная; b) U невырожденная и U*=U-1; c) UU* = En ; d) U* унитарная; e) столбцы в U образуют ортонормированную систему; f) строки в U образуют ортонормированную систему; g) для любого вектора x Є Cn справедливо x*x = (Ux)*(Ux) (т.е. унитарные матрицы - изометричные). Доказательство. а) влечет b), т.к. матрица U-1 (если она существует) - это единственная матрица, при умножении на которую слева получается E. Из определения унитарности следует, что U* именно такая матрица: UU* = UU-1 = E. Значит, из b) следует c). Так как c) - это определение унитарности для U*, то из c) следует d). Обращение импликаций проводится аналогично. Таким образом a), b), c) и d) эквивалентны. Обозначим ui - i-й столбец матрицы U. Из правил матричного умножения следует, что если U*U = E, то ui*uj = δij, где δij = Докажем, что из a) следует g). Возьмем y = Ux. Тогда y*y = x*U*Ux = x*x. Докажем, что из g) следует a). Рассмотрим сначала случай n = 2. Рассмотрим произвольную матрицу U, для которой выполняется g) для ∀x ∈ Cn. Возьмем
Имеем: 1 = x*x = y*y = x*U*Ux - это элемент матрицы U*U в позиции [1,1]. Аналогично полагая Тогда из g) следует 2 = x*x = y*y = x*U*Ux = Рассматривая 2 = x*x = y*y = x*U*Ux = 2 + i(a −  Таким образом Рассмотрим теперь случай n > 2. Пусть U ∈ Cn × n матрица, для которой выполняется g). Положим A = U*U. Возьмем x ∈ Cn, в котором все компоненты нулевые, кроме i-й и j-й (i ≤ j). Тогда
Случай n = 1 очевиден.
Унитарное подобие. Так как для унитарной матрицы U*=U-1 , то преобразование А → U*AU, определенное на Сn×n , явл. подобием которое называется унитарным подобием. Опр. Матрица B Є Сn × n называется унитарно подобной матрице А Є Сn × n , если найдется унитарная матрица U Є Сn × n , такая, что B = U*AU. Если Г можно выбрать вещественной (а значит, ортогональной), то В называется ортогонально подобной матрице А. Рассмотрим два специальных типа унитарных матриц, которые осуществляют преобразования унитарного подобия, весьма важные для вычисления собственных значений. Пример 1. (Плоские вращения). Матрица U(θ;i,j) осуществляет вращение (на угол θ) в плоскости координат i,j. Заметим, что если матрица умножается слева на U(θ; i, j), то в ней изменяются только i-я и j-я строки, а если она умножается справа, то изменяются только i-й и j-й столбцы. Таким образом, при переходе к унитарно подобной матрице, осуществляемом с помощью U(θ;i,j), происходит изменение только строк и столбцов с номерами i и j. Унитарное подобие, существляемое посредством плоских вращений, используется при вычислении собственных значений. Пример2. (Преобразования Хаусхолдера). Возьмем произвольный ненулевой вектор w ∈ Cn и образуем матрицу Uw = E – tww* (Uw ∈ Cn × n) , где t = 2(w*w)-1. Заметим, что w*w - это положительный скаляр, ww* ∈ Cn × n матрица. Если вектор w был нормирован (w*w = 1), то t должно быть равно 2, а матрица Uw должна иметь вид Uw = E − 2ww*. Часто образуют матрицу Uw, выбирая заранее именно нормированный вектор w. Любая матрица Uw называется преобразованием Хаусхолдера.
Теорема. Дляунитарно подобных матриц A и B из Сn×n имеет место равенство Доказательство:
18. Теорема Шура об унитарной триангуляризации матриц Теорема. (Шура об унитарной триангуляризации). Пусть задана матрица A ∈ Сn × n и зафиксирован какой-то порядок ее собственных значений λ1,... ,λn. Тогда существует унитарная матрица U ∈ Сn × n , такая, что U* AU = T = [tij] − верхняя треугольная матрица с диагональными элементами tii = λi, i = 1,n. Кроме того, если A ∈ Rn × n и все ее собственные значения вещественны, то U можно выбрать ортогональной. Другими словами, любая комплексная матрица унитарно подобна треугольной матрице. Доказательство:
Дополним x(1) до базиса: x(1), y(2) , , y(n) (*) Ортонормируем систему(*): x(1) , z(2) ,…, z(n) (**) Составим из (**) матрицу U1: унитарная U1 =[ x(1) , z(2) , . . . , z(n)] Рассмотрим матрицу:
Аналогично строится унитарная матрица Сформируем матрицу Продолжая аналогично, построим Замечание1. В формулировке теоремы Шура можно говорить не о верхних треугольных, а о нижних треугольных матрицах. При этом унитарная эквивалентность будет осуществляться другой матрицей U. Замечание2. В теореме Шура неоднозначно определяются и U, и T. Это связано с выбором векторов z(i), w(i) и т.п., порядком расстановки собственных чисел. Кроме того, то, что находится выше главной диагонали для унитарно подобных верхних треугольных матриц может сильно различаться. Применение теоремы Шура позволяет установить «почти диагонализуемость» произвольной матрицы.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 493. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
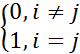 - символ Кронекера. Последнее равносильно тому, что ui,uj ортонормированные. Следовательно, a) равносильно e). Аналогично доказывается равносильность d) и f).
- символ Кронекера. Последнее равносильно тому, что ui,uj ортонормированные. Следовательно, a) равносильно e). Аналогично доказывается равносильность d) и f).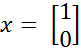
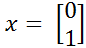 получим U*U(22) = 1. Т.е. U*U имеет вид
получим U*U(22) = 1. Т.е. U*U имеет вид  , где a - скалярное произведение 1-го и 2-го столбца,
, где a - скалярное произведение 1-го и 2-го столбца,  - 2-го и 1-го столбца. Положим
- 2-го и 1-го столбца. Положим 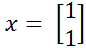

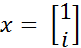 , будем иметь
, будем иметь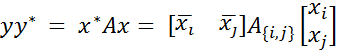 где A{j,j} главная подматрица матрицы A в строках i,j и столбцах i,j. Из доказанного выше при n = 2 следует, что A{j,j} = E2 ∈ Cn × n. Так как i,j - произвольные, то в A любая главная подматрица порядка 2 совпадает с E2. Единственная матрица, обладающая таким свойством - это матрица En.
где A{j,j} главная подматрица матрицы A в строках i,j и столбцах i,j. Из доказанного выше при n = 2 следует, что A{j,j} = E2 ∈ Cn × n. Так как i,j - произвольные, то в A любая главная подматрица порядка 2 совпадает с E2. Единственная матрица, обладающая таким свойством - это матрица En.
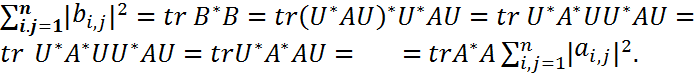

 Пусть x(1) - нормированный собственный вектор, отвечающий :
Пусть x(1) - нормированный собственный вектор, отвечающий : A[
A[ 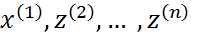 ]=
]=  [
[ 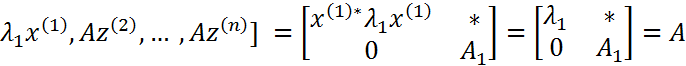
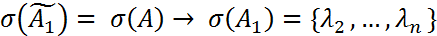
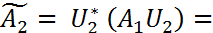
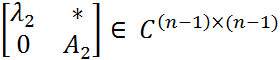
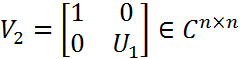

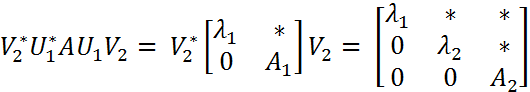
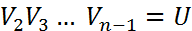 унитарная
унитарная