
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Спектральная теорема для нормальных матрицДля матрицы A = [ а) A нормальна; b) A унитарно диагонализуема; с) d) для А существует ортонормированная система из собственных векторов Доказательство. a) ⇒ b) : по теореме Шура существует унитарная матрица V ∈ Умножим это равенство на сопряженное. С учетом а) имеем
b) ⇒ a) : по определению унитарно диагонализуемой матрицы для матрицы A существуют унитарная матрица U ∈ Следовательно, с учетом свойства b) ⇒ c) следует из применения теоремы 5.4 (Для унитарно подобных матриц A и B из имеет место равенство c)⇒ b). По теореме Шура A =
а) ⇒ d) Обозначим U = [ Из разложения A = них равенств и определения собственных векторов вытекает, что  d) ⇒ a) Пусть A Составим из этих векторов матрицу U = [ AU = ΛU = UΛ, откуда следует
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 462. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ] ∈
] ∈ 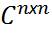 с собственными значениями λ1,... ,λn следующие утверждения равносильны:
с собственными значениями λ1,... ,λn следующие утверждения равносильны: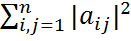 =
= 
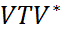 .
.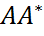 =
=  =
= 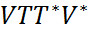 =
=  =
= 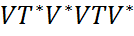 =
=  , откуда следует
, откуда следует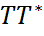 =
= 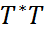 , т.е. T – треугольная нормальная матрица и по свойству
, т.е. T – треугольная нормальная матрица и по свойству 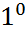 нормальных матриц (блочно-треугольная нормальная матрица T является блочно-диагональной.) T – диагональная.
нормальных матриц (блочно-треугольная нормальная матрица T является блочно-диагональной.) T – диагональная.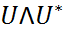 .
.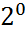 нормальных матриц (диагональная матрица является нормальной)
нормальных матриц (диагональная матрица является нормальной) 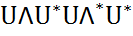 =
= 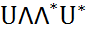 =
= 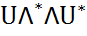 =
= 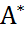 A, т.е. А – нормальная.
A, т.е. А – нормальная.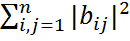 ) к унитарно подобным матрицам A и Λ.
) к унитарно подобным матрицам A и Λ.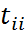 =
= 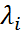 (A). Далее, применяя теорему 5.4 к унитарно подобным матрицам A и T, имеем:
(A). Далее, применяя теорему 5.4 к унитарно подобным матрицам A и T, имеем: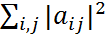 =
= 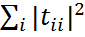 +
+ 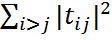 , откуда с учетом с) следует
, откуда с учетом с) следует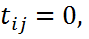 ∀ i < j.
∀ i < j.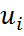 , i = 1,…, n – столбцы матрицы U в разложении A =
, i = 1,…, n – столбцы матрицы U в разложении A = 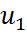
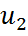 , . . . ,
, . . . , 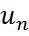 ] .
] .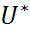 =
= 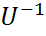 для унитарной матрицы U имеем AU = UΛ, что с учетом того, что матрица Λ – диагональная, равносильно A
для унитарной матрицы U имеем AU = UΛ, что с учетом того, что матрица Λ – диагональная, равносильно A 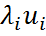 , i = 1,…, n. Из послед-
, i = 1,…, n. Из послед-