Ортогональное дополнение сопряженного пространства

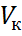Опр. Пусть  -произвольное подпространство векторного пространства 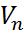. Множество ковекторов из 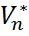, которые ортогональны всем векторам из , называется ортогональным дополнением к пространству  и обозначается : .

Другими словами, ортогональное дополнение к - это множество всех линейных функций из .,обращающихся в нуль на векторах из

К тому же, ортогональное дополнение к .

Теорема. Ортогональное дополнение подпространства  является подпространством пространства , при этом

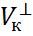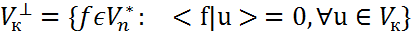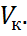
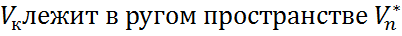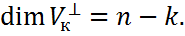
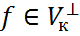Док-во. Пусть  - произвольный ковектор из ортогонального дополнения. Покажем, что ортогональность ковектора f всем векторам из  равносильна ортогональности fвекторам любого базиса в .

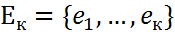Пусть  -некоторый базис в  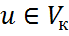тогда для любого вектора  справедливо разложение 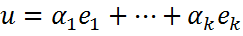, и в силу линейности функции f справедливо

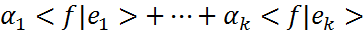 <f|u>== . Откуда следует, что <f|u>=0 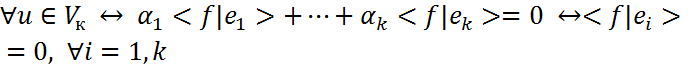(1)

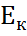Т.о. произвольный ковектор  является решением системы (1). Для заданного базиса  с базисными векторами вида  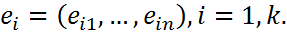система (1) равносильна системе линейных алгебраических уравнений:  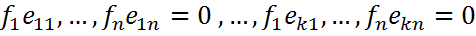(2).

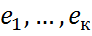Так как векторы  ЛНЗ, то ранг матрицы системы(2) равен k. как известно из линейной алгебры, множество решений системы (2) образует линейное пространство размерности n-k. Это равносильно доказываемому утверждению.

Сопряжённое отображение

Пусть дано линейное отображение А: → .

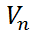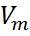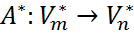Опр. Отображение  называется сопряженным отображением для А, если для любого  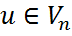и для любого  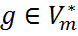выполняется следующее соотношение: .

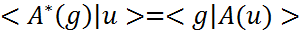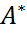Теорема. Для любого заданного линейного отображения А сопряженное отображение  существует, линейно и единственно.

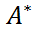Докво. Построим отображение  удовлетворяющему условию  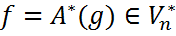для заданного отображения А. Для того чтобы задать отображение , надо для каждого функционала  указать соотвествующий ему функционал , являющийся образом g при отображение 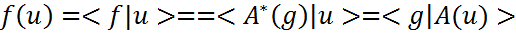. 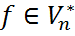Но надо задать функционал из .—это значит определить его действие на произвольный вектор . Зададим правило этого действия. С учетом определяющего соотношения  для сопряженного отображения имеем: .

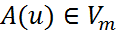Из этого следует, что для данного функционала  действие искомого функционала  на произвольный вектор  определяется следующим образом. Сначала применим отображение А: →  к вектору , в результате чего получаем его образ – вектор . Затем вычисляем значение заданного функционала  на векторе  и получаем значение <g|A(u)>, что является результатом действия f на u.

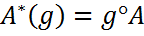Т.о. сопряженное отображение определяется как композиция . Т.к. выполняются эти условия: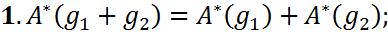 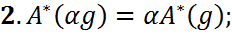, то можем утверждать, что данное отображение будет линейным.

Докажем единственность .

Пусть -- два отображения, для которых справедливо 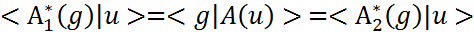. Тогда  для всех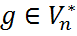 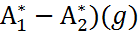. Отсюда следует, что <( |u>=0. Фиксируем g и будем менять u. Тогда элемент ( 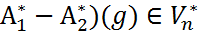. Как линейная функция на  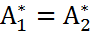принимает только нулевые значения, и, значит, равен нулю. Поэтому , что доказывает единственность и завершает доказательство теоремы.

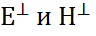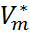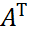Теорема. Пусть А: →  – линейное отображение Е и Н – базисы пространств  и , соответственно, - биортогональные базисы пространства  и . Тогда если отображение А в базисах Е и Н имеет матрицу А, то сопряженное отображение  в биортогональных базисах  и  имеет матрицу .