
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Унитарные и ортогональные матрицы. Их свойстваСистема векторов Теорема. Любая ортонормированная система ЛНЗ. Докво. Рассмотрим для ортонормированной системы векторов { Опр. Матрица Теорема. (о QR-разложении). Если Свойства унитарных матриц: 1. Для любых унитарных (ортогональных) матриц U, V 2. Все собственные значения унитарной матрицы по модулю равны 1. 3. Любая матрица перестановок – унитарная. Опр. Матрицей перестановок называется квадратная матрица, у которой по каждой строке и каждом столбце только один элемент отличен от нуля и равен единице. 4. Определитель унитарной матрицы по модулю равен 1 5. Унитарные матрицы одного порядка образуют группу по умножению.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 661. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
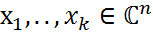 называется ортогональной, если
называется ортогональной, если 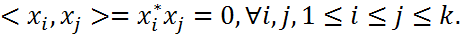 Если к тому же сами векторы нормированы, т.е.
Если к тому же сами векторы нормированы, т.е. 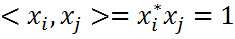 , i=1,k , то акая система называется ортонормированной.
, i=1,k , то акая система называется ортонормированной.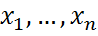 } равенство
} равенство 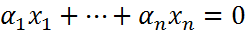 и покажем, что оно возможно лишь при
и покажем, что оно возможно лишь при  . Умножая равенство справа на сопряженное
. Умножая равенство справа на сопряженное 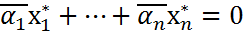 получим
получим 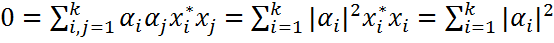 , что возможно только при
, что возможно только при 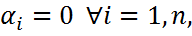 откуда и вытекает ЛНЗ системы {
откуда и вытекает ЛНЗ системы {  называется унитарной, если
называется унитарной, если 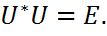 Если к тому же
Если к тому же 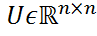 , то U называется ортогональной.
, то U называется ортогональной. , n>= m, то существуют матрица
, n>= m, то существуют матрица  c ортонормированными столбцами и верхняя треугольная матрица
c ортонормированными столбцами и верхняя треугольная матрица  , такие, что A=QR. Если m=n, то Q унитарна.
, такие, что A=QR. Если m=n, то Q унитарна. произведение UVявляется также унитарной(ортогональной) матрицей.
произведение UVявляется также унитарной(ортогональной) матрицей.