
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Эрмитовы и косоэрмитовы матрицы. Их свойства. Эрмитово разложениеМатрица A ∈ Свойства эрмитовых матриц: 1) Матрицы 2) Если матрица A эрмитова, то ее степень 3) Если A и B - эрмитовы, то матрица αA+βB эрмитова для любых вещественных α, β. 4) Матрица A − 5) Если A и B–косоэрмитовы, то матрица αA + βB косоэрмитова для любых вещественных α,β. 6) Если A - эрмитова, то iA - косоэрмитова. 7) 7). Если A - косоэрмитова, то iA - эрмитова. 8) Любую матрицу A ∈ A = 9) Если A − эрмитова, то все элементы на ее главной диагонали вещественны. Для того чтобы задать все Теорема (Об эрмитовом разложении). Любую матрицу A ∈ Доказательство. Существование представления следует из свойства 8), если положить B = H (A), C = S (A), свойства 6) и равенства C = −iiC (поскольку iC- эрмитова), а также свойства 7): H = H (A), T = −iC. Докажем единственность. Если A = K + iF - еще одно представление, где K и F - эрмитовы, то 2H = 
21. Критерии эрмитовости матрицы Матрица A ∈ а) функция b) матрица A нормальна и все ее собственные значения вещественны; с) матрица Доказательство. Необходимость. a) Рассмотрим число, комплексно-сопряженное к числу a) Таким образом, число x∗Ax совпадает с комплексно сопряженным числом b) Пусть λ - собственное значение эрмитовой матрицы A, x -соответствующий ему нормированный собственный вектор: b)Ax = λx, Умножим второе равенство на λ: λ = λ c) Для произвольной матрицы S ∈ c) Достаточность. Рассмотрим утверждение а) для вектора (x + y) ∈
Поскольку Возьмем в (6.1) x =
Возьмем x = i − i Из (6.2) и (6.3) следует, что b) По спектральной теореме для нормальных матриц нормальная матрица унитарно диагонализуема, т.е. A = Рассмотрим следовательно А - эрмитова. c) Положим S =
Теорема Рэлея-Ритца Теорема Рэлея-Ритца. Пусть A-эрмитова и ее собственные значения упорядочены (Пусть A – эрмитова,
Доказательство. Поскольку матр. А – эрмитова, то по спектральной теореме для эрмитовых матриц сущ. такие унитарные март. Каждый сомножитель
Поскольку март. U унитарна, а унитарные матр.изометричны, то имеют место равенства
Таким образом, справедливы соотношения:
что и доказывает (2). Покажем, что оценки в соотношении (2) точны. Действительно, если x – собст.векторматр. A, соответствующий собственному значению λ1, то
Точность оценки сверху устанавливается аналогично. Остальные утверждения является простыми следствиями соотношений(2). Покажем, например, справедливость (3). При Это неравенство обращается в равенство, когда x- собственный вектор матрицы A, соответствующий собственному значению Наконец, при
Таким образом, равенство (5) эквивалентно следующему
Рассуждения для минимального собственного значения
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 747. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
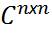 называется эрмитовой, если A =
называется эрмитовой, если A = 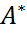 , и косоэрмитовой, если A = −
, и косоэрмитовой, если A = − 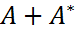 ,
, 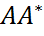 ,
, 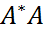 эрмитовы для любой матрицы A ∈
эрмитовы для любой матрицы A ∈ 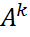 эрмитова для всех k = 1,2,.... Если A также невырожденная, то A−1тоже эрмитова.
эрмитова для всех k = 1,2,.... Если A также невырожденная, то A−1тоже эрмитова. (
( 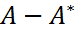 ) ≡ H(A) + S(A), где H(A) =
) ≡ H(A) + S(A), где H(A) =  элементов матрицы A, достаточно указать n вещественных чисел (диагональные элементы) и
элементов матрицы A, достаточно указать n вещественных чисел (диагональные элементы) и  комплексных чисел (внедиагональные).
комплексных чисел (внедиагональные).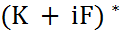 = K + iF +
= K + iF +  −
− 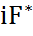 = 2K, откуда следует, что H = S. Аналогично устанавливается равенство F = T и существование единственного представления A = B + C.
= 2K, откуда следует, что H = S. Аналогично устанавливается равенство F = T и существование единственного представления A = B + C.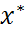 Ax принимает вещественные значения для любого x ∈
Ax принимает вещественные значения для любого x ∈ 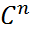 ;
;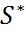 AS эрмитова для любой матрицы S ∈
AS эрмитова для любой матрицы S ∈  =
= 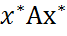 =
= 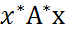 =
= 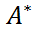 = A) =
= A) =  .
.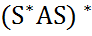 =
= 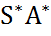 S =
S = 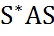 , следовательно
, следовательно 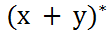 A(x + y) = (
A(x + y) = ( 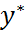 Ay) + (
Ay) + ( 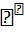 .
.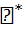 Ax ∈ R,
Ax ∈ R,  , y =
, y = 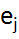 (
( 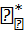 A
A 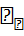 +
+ 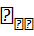 +
+ 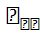 = Re
= Re 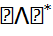 , где U ∈
, где U ∈ 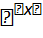 - унитарная матрица, Λ = diag{
- унитарная матрица, Λ = diag{ 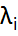 , ..,
, .., 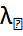 }∈
}∈ 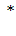 =
= 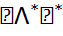 =
= 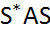 = (
= ( 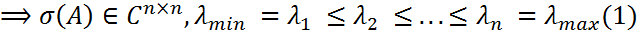 ). Тогда
). Тогда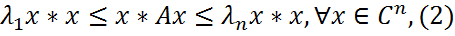

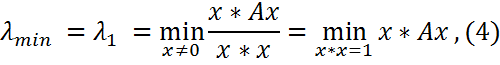
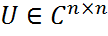 и диагональная матрица
и диагональная матрица 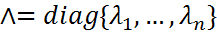 , что
, что 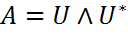 . При любом векторе
. При любом векторе 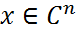 верны равенства
верны равенства 
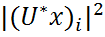 неотрицателен, поэтому
неотрицателен, поэтому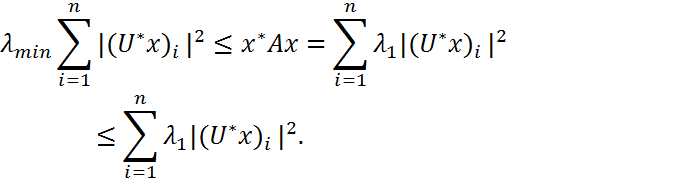

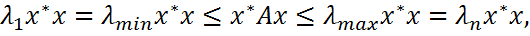
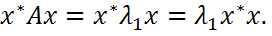
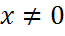 из правой части соотношения (2) имеем:
из правой части соотношения (2) имеем: 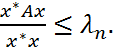
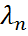 . Следовательно,
. Следовательно, 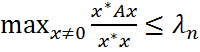 .(5)
.(5)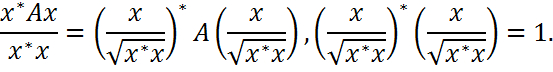
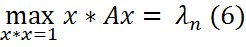
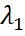 аналогичны.
аналогичны.