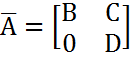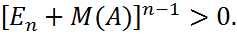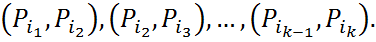Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уточнение оценок собственных значений с помощью преобразования подобия.Если относительно матрицы имеется некоторая дополнительная информация, в силу которой собственные значения принадлежат (или не принадлежат) конкретным множествам, то в сочетании с теоремой Гершгорина эта информация может привести к более точной локализации собственных значений. Определяющие свойства некоторых типов матриц и свойства их собственных значений приведены в таблице
Следствие. Пусть
Пусть
33. Локализация собственных значений Неравенство Шура. Теорема Бендиксона. Теорема (Неравенство Шура). Если A = (aij) ∈
причем равенство имеет место тогда и только тогда, когда матрица А нормальная. Доказательство. Согласно теореме Шура сущ. унитарная матрица
Поскольку след у подобных матриц равен, то trAA∗ =trTT∗ (2) Далее с учётом (2) справедливы соотношения
что и доказывает (1). Равенство возможно тогда и только тогда, когда
Теорема (Бендиксона). Если
Доказательство. Пусть x - нормированный собственный вектор матрицы A, соответствующий собственному значению λk : Ax=λkx, x*x=1. (1).  Тогда (Ax)*x=x*A*x=(λkx)*x= Т. к. матр. Bэрмитова, то для нее справедлива теор Рэлея-Ритца:
Отсюда с учетом первого соотношения теоремы Рэлея-Ритца имеем
Аналогично, применяя теоремуРэлея-Ритца к эрмитовой матрице C, получим второе соотношение теоремы.
Локализация собственных значений Теорема Гирша. Теорема Брауна. Теорема (Гирша). Если
Доказательство. Согласно теореме Шура сущ. м-цы U - унитарная, T - треугольная, такие, что U*AU =T, tii=λi. Тогда верно: U*A*U =T*,
Длядиагональныхэлементовматрицверно
Согласно (4) с учетом инвариантноcти следа относительно преобразования подобия имеем:
Тогда Аналогично доказывается (3). Теорема(Брауна). Если Доказательство. ПустьAx=λix, x∈C, x*x=||x||22=1 (2) Тогда ||Ax||22 =||λix||22= |λi|2||x||22 =|λi|2 Получаем: |λi|2=||Ax||22=(Ax)*Ax=x*A*Ax. По теореме Рэлея-Ритца для эрмитовой матрицы A*A верно: λmin(A*A)x*x≤x*(A*A)x≤λmax(A*A), откуда с учетом λmin(A*A)=σn2, λmax(A*A)=σ12и (2) следует справедливость (1).
Невырожденность матриц. Определение. Матрица
Теорема(Адамара).Если А – матрица со строгим диагональным преобладанием, то она обратима. Теорема. Если у матрицы Определение. Матрица
где B и D - квадратныематрицы. В противномслучаематрица A называется неразложимой. Определение. Матрица M(A) с элементами (8.25) называется индикаторной матрицей для A. Теорема. Матрица Определение. Ориентированным путём в графе Г из вершины Pi1в вершину Pik наз.последовательность дуг Длина ориентированного пусть – это чисто луг в нём, если оно конечно. ОпределениеОриентированный граф называется сильно связным, если в нем любые два узла Pi,Pj соединены ориентированным путем конечной длины, начинающимся в Pi изаканчивающимся в Pj. Теорема .Матрица Следствие Матрица, у которой все элементы ненулевые, неразложима. Теорема Ольги Тауски. Если для неразложимой матрицы А выполняются ослабленные условия Адамара и по крайней мере в одном из этих условий имеет строгого неравенства(>), то матрица А – невырожденная. |
|||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 544. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
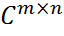 AAT=ATA=En
AAT=ATA=En
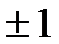 .
.
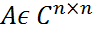 и пусть p1,p2,…,pn- произвольные положительные числа. Все собственные значения матрицы A принадлежат каждой из двух областей
и пусть p1,p2,…,pn- произвольные положительные числа. Все собственные значения матрицы A принадлежат каждой из двух областей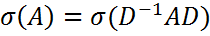
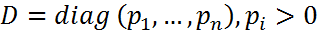
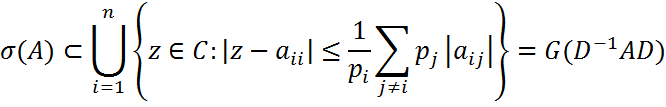
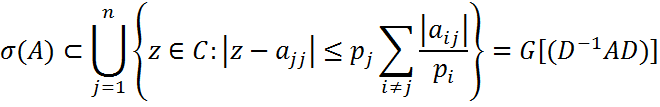
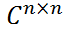 имеет собственные значения λ1,…,λn, то
имеет собственные значения λ1,…,λn, то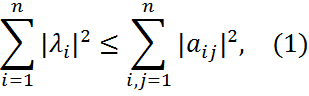
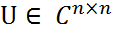 , такая, что U*AU =T, где T – верхняя треугольная матрица с диагональными элементами tii=λi, i=1,n. Тогда
, такая, что U*AU =T, где T – верхняя треугольная матрица с диагональными элементами tii=λi, i=1,n. Тогда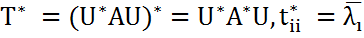 ,а значит
,а значит т.е. матрицыAA∗и TT∗подобны.
т.е. матрицыAA∗и TT∗подобны.
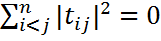 , т.е. тогда итолько тогда, когдаматрицаA– нормальная.
, т.е. тогда итолько тогда, когдаматрицаA– нормальная.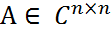 ,то
,то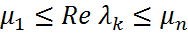
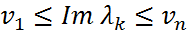
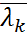 x*x.(2).
x*x.(2).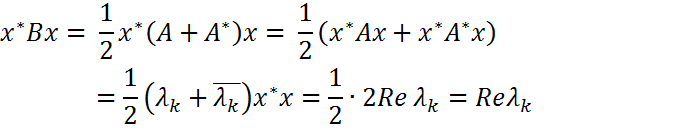
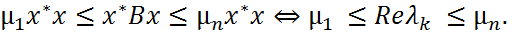
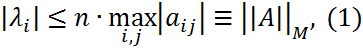
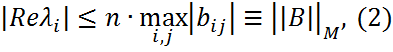
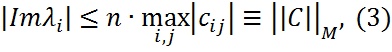
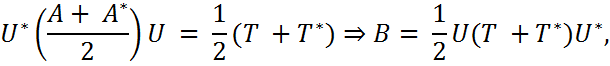
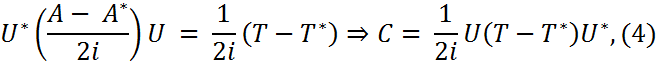
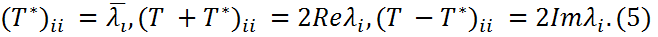

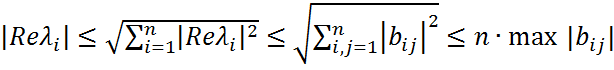 .
.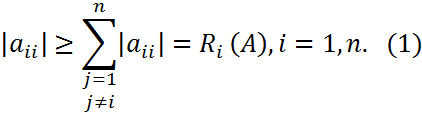
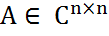 все диагональные элементы ненулевые и она является матрицей с диагональным преобладанием, причем для всех, кроме одного, значений i=1,2,..,n это свойство выполняется в сильной форме, т.е. |aii|>Ri(A), то А обратима.
все диагональные элементы ненулевые и она является матрицей с диагональным преобладанием, причем для всех, кроме одного, значений i=1,2,..,n это свойство выполняется в сильной форме, т.е. |aii|>Ri(A), то А обратима.