
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нормальное псевдорешение системы линейных алгебраических уравнений.Опр. Вектор r=b-Ax называется невязкой вектора х. Длина невязки ||r|| характеризует, насколько вектор х близок к решению систему. Если х является решением системы, то невязка равно нулю. Если система несовместна, то невязка всегда будет ненулевой. В этом случае можно поставить задачу: найти такой вектор х0, что величина ||r||2=||b-Ax0||2 примет наименьшее значение. Такой подход называют методом наименьших квадратом. Опр. Вектор х0, длина невязки которого минимальна, наз. Псевдорешением системы Ах=b. Псевдорешение с минимальной длиной называется нормальным псевдорешением системы Ax=b. Теорема. Нормальное псевдорешение системы Ах=b всегда существует, единственно и определяется по формуле х0 =
10. Матричные уравнения AX = XB Рассмотрим матричное уравнение AX=XB, Рассмотрим элементарные делители матрицы А:
Теорема. Общее решение уравнение АХ=ХВ, где A=U
Если Матрица Х зависит от N произвольных параметров
Следствие. Если матрицы А и В не имеют одинаковых собственных значений, то уравнение АХ=ХВ имеет только нулевое решений, то есть Х=0.
11. Матричные уравнения AX = XA Рассмотрим частный случай уравнения АХ=ХВ при В=А: АХ=ХА Теорема. Общее решение АХ=ХВ, где Если
Теорема. Число ЛНЗ матриц, перестановочных с матрицей  Замечание. Ясно, что m=n1+n2+…+nt. Отсюда следует, N≥m, причем N=m равносильно t=1, то есть все элементарные делители матрицы А взаимно просты.
Сопряженное пространство и его базис Пусть Опр. Числовая функция y=f(u) с аргументами из
Опр. Пространство линейных функций, определенных на векторном пространстве Функции из пространства Опр. Вектор u и ковектор f называются ортогональным друг другу, если <f|u>=0. Функционалы Теорема. Координатные функционалы Следствие. Для любого базиса Е пространства Опр. Базис и F={
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 696. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
. и элементарные делители матрицы В:
и элементарные делители матрицы В: .
.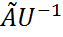 , B=V
, B=V 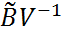 ,
,
 , может быть найдено по формуле Х=U
, может быть найдено по формуле Х=U 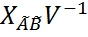 . Здесь
. Здесь  -общее решение уравнение
-общее решение уравнение 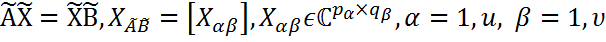
 , то
, то 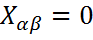 , если
, если 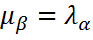 , то
, то  - произвольная верхняя треугольная матрица.
- произвольная верхняя треугольная матрица.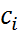 : Х=
: Х=  , где
, где  ,
,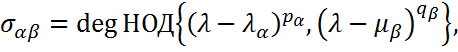
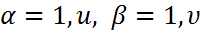
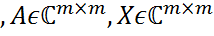 .
.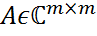 , А=U
, А=U 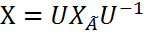 . Здесь
. Здесь 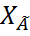 -общее решение ур-ния.
-общее решение ур-ния. 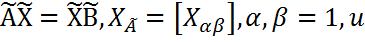 .
.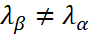 , то
, то  , то
, то  , где
, где
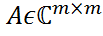 , определяется формулой N=n1+3n2+5n3+…+(2t-1)nt, где
, определяется формулой N=n1+3n2+5n3+…+(2t-1)nt, где 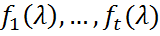 - непостоянные инвариантные множители матрицы А,
- непостоянные инвариантные множители матрицы А,  .
.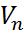 – линейное векторное пространство над полем
– линейное векторное пространство над полем 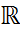 ,
,  .
.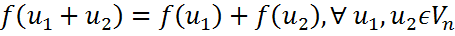 ;
;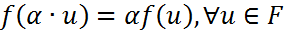 .
.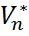 .
. называются координатными функционалами базиса {
называются координатными функционалами базиса { 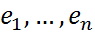 }. Для них
}. Для них 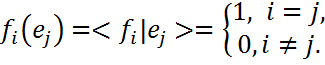 (1). Соотношение (1) называются соотношениями биортогональности, а система векторов E={
(1). Соотношение (1) называются соотношениями биортогональности, а система векторов E={  }, удовлетворяющие (1) –биортогональными, что обозначаются как E
}, удовлетворяющие (1) –биортогональными, что обозначаются как E  F.
F.