
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема о единственности псевдообратной матрицы Мура-ПенроузаОпр. Матрица Теорема. Для любой матрицы А псевдообратная матрица Мура-Пенроуза существует, единственна и выражается по формуле Док-во: Докажем, что для данной матрицы А не существует двух различный псевдообратных матриц Введем обозначение Тогда имеем АDA=0, D=U Таким образом, единственность псевдообратной матрицы, а значит и теорема доказана. Свойства псевдообратной матрицы Мура-Пенроуза Свойства: 1. 2. 3. 4. 5. 6. Матрица А, 7. 8. 9. Докво.: Для док-ва 1 используем представление
Далее заметим, что для матрицы Получаем равенство этих формул. Докажем 3 св-во
Далее с учетом св-в операций * получим Аналогично доказывается 4. Свойство 5 доказывается непосредственно с применением Докажем 6. Т.к. ранг произведение матриц не превосходит ранга любого из сомножителей, то из А rk A=rk A 7 и 8 вытекают из
Решение однородных систем линейных алгебраических уравнений с использованием псевдообратной матрицы Мура-Пенроуза  Теорема. Общее решение однородной системы Ах=0 задается равенством Докво: Во-первых, для любого вектора q справедливо Следствие. Решение системы Ах=0 единственно тогда и тока когда матрица А имеет полный ранг по столбцам. Док. Действительно, в этом случае из 8 св-ва вытекает Если решение не единственно, то существует бесконечно много решений, задаваемых формулой х=
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 542. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 называется псевдообратной матрицей Мура-Пенроуза для матрицы
называется псевдообратной матрицей Мура-Пенроуза для матрицы  , если выполнимы следующие условия:
, если выполнимы следующие условия:  ,
,  , где
, где  ,
,  - некоторые матрицы.
- некоторые матрицы.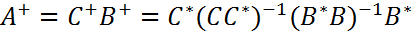 , где В и С- компоненты скелетного разложения А=ВС матрицы А.
, где В и С- компоненты скелетного разложения А=ВС матрицы А.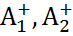 . Действительно:
. Действительно:  , откуда получаем
, откуда получаем 

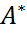 =
=  . => (DA)*DA=A*D*DA=A*V*ADA=0., что равносильно
. => (DA)*DA=A*D*DA=A*V*ADA=0., что равносильно  .
.

 А
А  -эрмитова
-эрмитова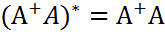 , т.е. матрица
, т.е. матрица  эрмитова
эрмитова
 имеют один и тот же ранг.
имеют один и тот же ранг. , если А имеет полный ранг по строкам.
, если А имеет полный ранг по строкам. , если А имеет полный ранг по столбцам
, если А имеет полный ранг по столбцам .
. С учетом св-во операции * имеем:
С учетом св-во операции * имеем:
 является скелетным разложением. Используя для
является скелетным разложением. Используя для 
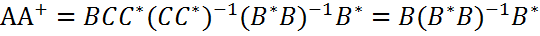 .
. сравнивая результаты, убеждаемся в справедливости 3.
сравнивая результаты, убеждаемся в справедливости 3. ;
;  отсюда следует rk A=rk
отсюда следует rk A=rk 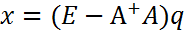 , где q- произвольный вектор подходящего размера.
, где q- произвольный вектор подходящего размера. Это означает, что х-решение системы Ах=0. Во-вторых, для любого решения х системы Ах=0 найдется вектор q, при котором х имеет представление х=
Это означает, что х-решение системы Ах=0. Во-вторых, для любого решения х системы Ах=0 найдется вектор q, при котором х имеет представление х=  . Действительно, можно просто положить q=x, т.к.
. Действительно, можно просто положить q=x, т.к.  . Теорема доказана.
. Теорема доказана. и из х=
и из х=