
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема о существовании псевдообратной матрицы Мура-Пенроуза.Стр 1 из 14Следующая ⇒ Функции от матриц. Простейшими функциями от матриц являются полиномы. Если задан числовой полином относительно
Рассмотрим теперь произвольную функцию
Опр. Если для функции Если функция f не определена на спектре матрицы А, то не определенно и f(A). Лемма. Значения полиномов g(λ) и h(λ) на матрице А совпадают тогда и только тогда, когда они имеют одинаковые значения на спектре матрицы А. Опр. Пусть функция f определена на спектре матрицы А. Тогда f(A)=g(A), где
Интерполяционный полином Лагранжа-Сильвестра Опр. Полином r(λ) , определяемый интерполяционными условиями Называется интерполяционным полиномом Лангранжа-Сильвестра функция Опр. Если функция f(λ) определена на спектре матрицы А, а r(λ) - соответствующий интерполяционный полином Лагранжа-Сильвестра, то f(А) = r(А). Виды интерполяционный полином Лангранжа-Сильвестра: 1. где все собственные значения различны: 2. есть кратные собственные, но минимальный имеет простые корни: 3. минимальный имеет кратные корни:
Свойство функции матрицы:  1. Если 2. Если две матрицы А и В подобны и матрица S преобразует А в В: 3. Если А- блочно-диогональная матрица: A=diag{A1,A2,…,Au}, то f(A)=diag{f(A1),f(A2),…,f(Au)}.
Скелетное разложение матрицы: лемма о ранге, лемма о существовании и неединственности скелетного разложения Опр. Пусть Лемма. В скелетном разложение А=ВС rkB=rkC=rkA=r(1). Докво. Ранг произведения двух матриц не превосходит рангов сомножителей. Поэтому, r=rk A=rk BC<=min{rk B, rk C} (2). Но Rk B<=r, rk C<= r, поскольку r – один размеров матриц В и С. Отсюда и из (2), следует (1). Лемма. Для любой матрицы Замечание. Если матрица Лемма. Скелетное разложение матрицы А неединственно. Док-во. Если вместо матрицы В и С в А=ВС взять В1=BS, С1=S-1C, где S- любая невырожденная r*r – матрицы, то А=B1C1 – представление того же вида А=ВС. 4. Свойства компонент скелетного разложения A=BC: лемма о невырожденности В*В, СС* Лемма. Если В и С – компоненты скелетного разложения А=ВС, то матрицы В*В и СС* - невырожденные. Докво. Пусть х-произвольное решение уравнения В*Вх=0. Покажем, что оно может быть только нулевым. Умножим уравнение В*Вх=0 слева на х*: х*В*Вх=(Вх)*Вх=0, что равносильно Вх=0. Согласно лемме о ранге – это однородная система с матрицей полного ранга по столбцам, поэтому из Вх=0 следует х=0. Отсюда, вытекает что det B*B≠0. Невырожденность СС* доказывается аналогично.
Теорема о существовании псевдообратной матрицы Мура-Пенроуза. Опр. Матрица Теорема. Для любой матрицы А псевдообратная матрица Мура-Пенроуза существует, единственна и выражается по формуле Док-во: Докажем существование матрицы
Умножим последнее равенство слева на В*:
Теперь умножая последнее равенство справа на В*, получим Рассмотрим матрицу Тогда используя А=ВС и
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 428. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , то f(A), A
, то f(A), A  , находиться непосредственной подстановкой:
, находиться непосредственной подстановкой: .
. скалярного аргумента
скалярного аргумента  . Пусть
. Пусть (1)― минимальный полином матрицы А степени
(1)― минимальный полином матрицы А степени  . Здесь
. Здесь 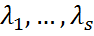 ― все различные собственные значения матрицы А:
― все различные собственные значения матрицы А:  .
. (k=1,s) из (1) определены производные
(k=1,s) из (1) определены производные  (2), то говорят, что функция
(2), то говорят, что функция  матрицы А. Совокупность этих значений будем символически обозначать f[δ(A)].
матрицы А. Совокупность этих значений будем символически обозначать f[δ(A)]. - любой полином, принимающий на спектре матрицы А те же значения, что и
- любой полином, принимающий на спектре матрицы А те же значения, что и  ,
,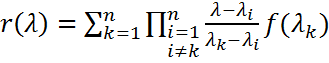


 , где
, где 

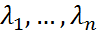 - собственные значения матрицы n-го порядка А, то
- собственные значения матрицы n-го порядка А, то  - полная система соб. Значений матрицы f(A).
- полная система соб. Значений матрицы f(A). то матрица f(A), f(B) подобны и та же матрица S преобразует f(A) в f(B): f(B)=S-1 f(A)S.
то матрица f(A), f(B) подобны и та же матрица S преобразует f(A) в f(B): f(B)=S-1 f(A)S. , rank A=r>0. Представление A=BC, где
, rank A=r>0. Представление A=BC, где  ,
,  называется скелетным разложением матрицы А.
называется скелетным разложением матрицы А. существуют скелетное разложние.
существуют скелетное разложние.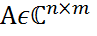 имеет полный ранг по столбцам rkA=n (или по строкам rkA=m), то в качестве матрицы В удобно взять саму матрицу А, а в качестве матрицы С-матрицу А.
имеет полный ранг по столбцам rkA=n (или по строкам rkA=m), то в качестве матрицы В удобно взять саму матрицу А, а в качестве матрицы С-матрицу А. называется псевдообратной матрицей Мура-Пенроуза для матрицы
называется псевдообратной матрицей Мура-Пенроуза для матрицы  , если выполнимы следующие условия:
, если выполнимы следующие условия:  ,
,  , где
, где  ,
,  - некоторые матрицы.
- некоторые матрицы.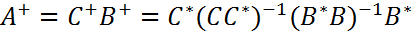 , где В и С- компоненты скелетного разложения А=ВС матрицы А.
, где В и С- компоненты скелетного разложения А=ВС матрицы А. Если А=0, положим
Если А=0, положим  . Пусть А≠0. Рассмотрим разложение А=ВС и будем искать сначала
. Пусть А≠0. Рассмотрим разложение А=ВС и будем искать сначала  Из определения псевдообратной мтарицы имеем:
Из определения псевдообратной мтарицы имеем: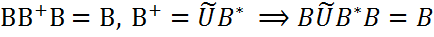 .
.
 , аналогично получаем
, аналогично получаем  .
. и покажем, что она удовлетворяет условиям
и покажем, что она удовлетворяет условиям  .
.
 ,
,  , где
, где 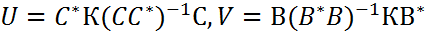 .
.