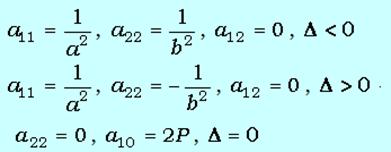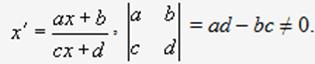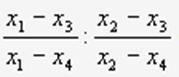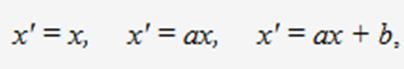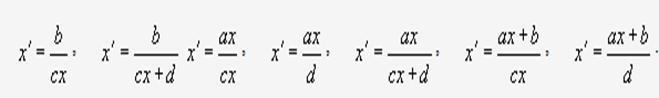Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Неподвижные точки при аффинном преобразовании ⇐ ПредыдущаяСтр 10 из 10 Пусть дана f:
Тогда нужно решить систему (1) Рассматривая систему (1) аффинное преобразование может иметь одну неподвижную точку, не иметь неподвижных точек или иметь бесконечное множество неподвижных точек. Система (1) имеет одну неподвижную точку, если
35Прямолинейные образующие однополостного гиперболоида. Дано:  Легко подсчитать, что в каждой из систем уравнений (3), (4) ранг матрицы, составленной из коэффициентов при x, y, z равен двум, то есть системы (3), (4) определяют прямую при фиксированных k1,l1,k2,l2. Свойства: 1. Через каждую точку однополостного гиперболоида проходят две и только две прямолинейные образующие. 2. Любые две прямолинейные образующие одного семейства скрещиваются. 3. Любые две прямолинейные образующие из разных семейств лежат в одной плоскости.
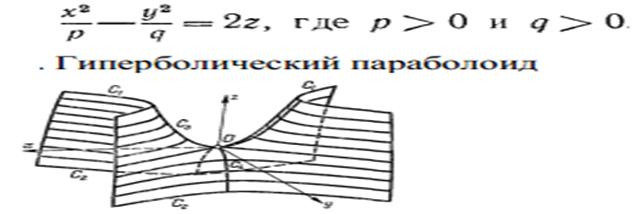
Прямолинейные образующие гиперболического параболоида. Уравнение:
2.Плоские линии, определяемые уравнением второй степени, не содержащим члена с произведением переменных. Способы аналитического задания: Эллипс - плоская линия. Уравнение в прямоугольных координатах: линия расстояний каждой точки Р которой до двух фиксированных точек F1 и F2 (фокусов) постоянна и равна2a . Уравнение в прямоугольных координатах: - X 2/a2 +Y2/a2=1 Гипербола— плоская линия, разность расстояний каждой точки Р которой до двух фокусов F1 и F2 постоянна и равна 2 а или —2 а. Уравнение в прямоугольных координатах: X2/A2-Y2/B2=1 Парабола— плоская линия, расстояние каждой точки Р которой до фокуса F равно расстоянию до фиксированной прямой d. Уравнение в прямоугольных координатах: Y2=2PX Асимптотические направления относительно линии второго порядка. Линии эллиптического, гиперболического, параболического типа. Способы аналитического задания: Направление, определяемое ненулевым вектором называется асимптотическим направлением относительно линии γ (1), если прямая || либо имеет с γ не более одной общей точки, либо содержится в γ. При решении квадратного уравнения ( 26.Понятие о группе аффинных преобразований и ее подгруппах. Проективным называется преобразование вида: Совокупность этих преобразований образует пространственную группу. Геометрия, основанная на проективных преобразованиях, называется проективной. Инвариантом проективной группы является двойное, или ангармоническое, отношение четырех точек: Подгруппы - преобразования, которые получают обнулением одного, двух или трех коэффициентов. Имеем девять подгрупп:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 861. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
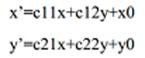
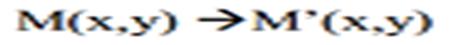
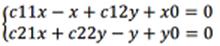
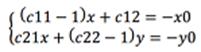
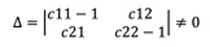 Если дельта равна 0 и х0=у0=0, то аффинное преобразование имеет бесчисленное множество неподвижных точек. Если дельта не равна 0 и х0=у0=0, то аффинное преобразование не имеет неподвижных точек.
Если дельта равна 0 и х0=у0=0, то аффинное преобразование имеет бесчисленное множество неподвижных точек. Если дельта не равна 0 и х0=у0=0, то аффинное преобразование не имеет неподвижных точек.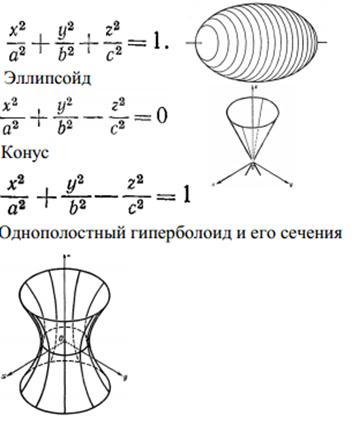
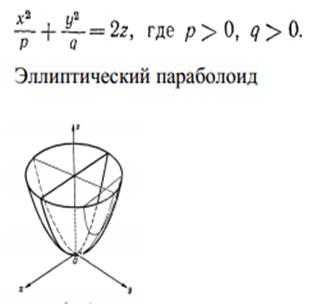

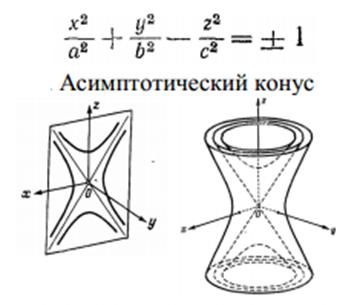
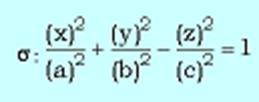 - напоминает уравнение однополостного гиперболоида. Преобразуем его:
- напоминает уравнение однополостного гиперболоида. Преобразуем его: 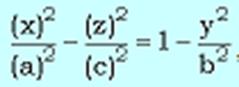
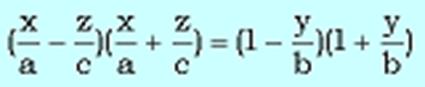 Рассмотрим две системы уравнений:
Рассмотрим две системы уравнений: 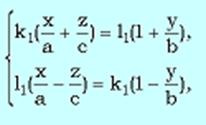 и
и 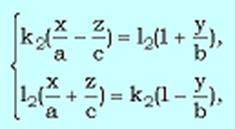 где
где 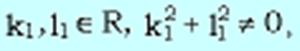 и
и 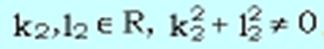
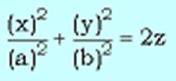 или
или 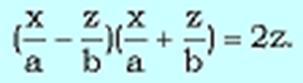 Рассмотрим две системы уравнений:
Рассмотрим две системы уравнений: 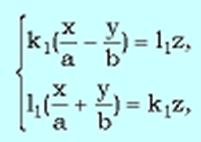 и
и 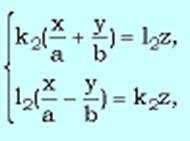 Где k1,l1,k2,l2 принадлежат R, k1^2+l1^2<>0, k2^2+l2^2<>0. Прямолинейные образующие гиперболического параболоида обладают свойствами 1 – 3, аналогичные свойствам однополостного гиперболоида.
Где k1,l1,k2,l2 принадлежат R, k1^2+l1^2<>0, k2^2+l2^2<>0. Прямолинейные образующие гиперболического параболоида обладают свойствами 1 – 3, аналогичные свойствам однополостного гиперболоида. 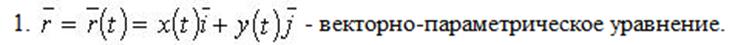

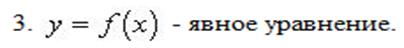
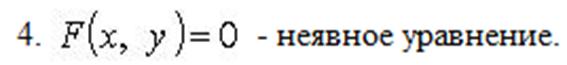
 ),
), 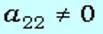 возможны случаи:
возможны случаи: 
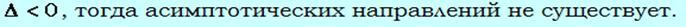

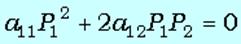 ,
, 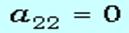 :
: 
 В зависимости от delta линии второго порядка относят к линиям эллиптического типа (delta<0), гиперболического типа (delta>0), параболического типа (delta=0).
В зависимости от delta линии второго порядка относят к линиям эллиптического типа (delta<0), гиперболического типа (delta>0), параболического типа (delta=0).