
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Выражение координат образа данного вектора при аффинном преобразовании плоскости (пространства).Координаты в аффинном пространстве Аn вводятся точно так же, как это делалось в случаях аффинных координат на плоскости и в пространстве Е3. Опр Аффинной системой координат или репером в аффинном пространстве Аn называется упорядоченная система (О, е1, е2,…, еn) (1), состоящая из некоторой точки О Теорема. Координаты точки в заданном репере определены однозначно. Пусть наряду с точкой М задана еще одна точка N с координатами y1,y2,…,yn (4) в том же репере (1). Тогда
Запишем формулы (9) в развернутом виде x1=а11х’1+а12х’2+a1nx’n+a1, xn=an1x’1+an2x’2+…+annx’n+an  или в виде xi = Формулы (9) — (11) называются формулами преобразования аффинных координат. Они выражают координаты произвольной точки в некотором репере (1) через координаты этой же точки в другом репере (5).
31.Ассимптотический конус. Рассмотрим урав-ние Значения a,b,c-одинаковые. Рассмотрим сечение заданных поверхностей плоскостью z=h,) |h|>c.
Эллипсы в сечении будут расположены: ‘эллипс в сечении однопол. гипер. будет содержать внутри эллипс,полученный в сечении конуса и эллипса в сечении двуполос. гипер. Рассмотрим
Аналогично можно показать, что 32.Эллиптический параболоид. Сечения эллиптического параболоида и его образование. Опр Эллиптическим параболоидом называется фигура, которая в прямоугольной системе координат задается уравнением то весь параболоид расположен по одну сторону от плоскости Оху. Рассмотрим пересечение параболоида (1) с плоскостью z=h. (2) Проекция на плоскость Оху множества Ф1 точек, получающихся в пересечении параболоида (1) с плоскостью (2), задается уравнением множество Ф1 в этом случае содержит лишь эту точку. При h > 0 множество Ф1 есть эллипс с полуосями a= х = l. (4).Проекция этого множества на плоскость Оyz задается в системе координат Оyz уравнением y2 = 2qz—ql2/p. (5) .Аналогичная картина получается при пересечении параболоида (1) с плоскостью y=m (6) Проекция соответствующего сечения на плоскость Оxz имеет в системе координат Охz уравнение х2 = 2pz — pm2/q. При различных m сечения являются параболами одинаковых размеров (с параметром р). Таким образом, можно получить следующий способ построения эллиптического параболоида: если взять две параболы, плоскости которых взаимно перпендикулярны, а оси имеют одинаковое направление, и одну из этих парабол (образующую) передвигать поступательно так, чтобы ее вершина скользила по другой параболе (направляющей), то образующая парабола опишет эллиптический параболоид. Если поменять ролями образующую и направляющую параболы, то получится тот же параболоид. Величины р и q эллиптического параболоида (1) (рис.) называются параметрами параболоида, а начало координат — его вершиной. Если p=q, фигура (1) называется параболоидом вращения. Она может быть получена вращением параболы х2 = 2рz, расположенной в плоскости Oxz, вокруг оси Оz
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 280. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Аn и базиса е1, е2,…еn (2) соответствующего линейного пространства Vn. Координатами точки М
Аn и базиса е1, е2,…еn (2) соответствующего линейного пространства Vn. Координатами точки М  в базисе (2), т. е. коэффициенты в разложении
в базисе (2), т. е. коэффициенты в разложении  =y1e1+у2е2+...+уnеn тогда
=y1e1+у2е2+...+уnеn тогда 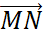 =
=  в базисе (2) равен X-A1, а в базисе (6) равен X', по формулам преобразования координат вектора имеем: X — А1=АХ' или X=AX’+A1 (9)
в базисе (2) равен X-A1, а в базисе (6) равен X', по формулам преобразования координат вектора имеем: X — А1=АХ' или X=AX’+A1 (9) (10)
(10) i=1,2,…,n (11)
i=1,2,…,n (11)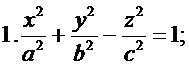 (однополосный гиперболойд);
(однополосный гиперболойд); 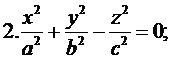 (конус);
(конус);  (двуполосный гиперболойд)
(двуполосный гиперболойд) - эллипс;
- эллипс;  - полуоси;
- полуоси; -эллипс;
-эллипс; 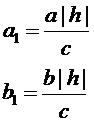 - полуоси;
- полуоси;
 - полуоси;
- полуоси;

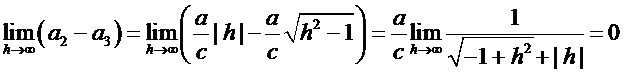 .
. . При
. При  в сечении получаются эллипсы, у которых полуоси стремятся друг к другу, но не будут совпадать. Конус находится внутри однопол. гипер.а двупол. гипер. внутри конуса. Тогда конус наз. ассимптотическим конусам к однопол. и двупол. гиперболойду.
в сечении получаются эллипсы, у которых полуоси стремятся друг к другу, но не будут совпадать. Конус находится внутри однопол. гипер.а двупол. гипер. внутри конуса. Тогда конус наз. ассимптотическим конусам к однопол. и двупол. гиперболойду. +
+  =2z, (1) где p>0, q>0. Параболоид (1) симметричен относительно координатных плоскостей Oxz, Оyz и оси Оz. Так как из уравнения (1) следует, что z>0,
=2z, (1) где p>0, q>0. Параболоид (1) симметричен относительно координатных плоскостей Oxz, Оyz и оси Оz. Так как из уравнения (1) следует, что z>0, , b=
, b=  . Если h растет, то полуоси а и b увеличиваются, и эллипс, получающийся в сечении, неограниченно расширяется. Исследуем множество Ф1 точек, получающихся в пересечении параболоида (1) с плоскостью
. Если h растет, то полуоси а и b увеличиваются, и эллипс, получающийся в сечении, неограниченно расширяется. Исследуем множество Ф1 точек, получающихся в пересечении параболоида (1) с плоскостью