
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Однополосный гиперболоид и его свойства.
где a>0,b>0,c>0. При a=b одн-ный гип-ид назыв. однополостным гиперболоидом вращения, т.к. он может быть получен вращением гиперболы вокруг мнимой оси. Свойства: 1.Симетричность (относительно: координатных плоскостей, координатных осей и начало координат) 2. Форма:a)Oxy, z=0, z=m, m>0, m→∞ - полуоси у эллипса увеличиваются b)Oxz, y=0, n>b, -гипербола с мнимой осью параллельной оси Ox n=b, - пара пересекающихся прямых 0<n<b, - гипербола с мнимой осью параллельной оси Oz Аналогично рассматривается сечения поверхности плоскостью х=0 (Ozy)и ей параллельными плоскостями. 30. Двуполостный гиперболоид и его свойства.
где a>0,b>0,c>0.
Если a=b – двуп. гиперб. вращения, т.к. может быть получен вращением гиперболы вокруг действ. оси. Свойства: 1.Симетричность (относительно: координатных плоскостей, координатных осей и начало координат) 2.Форма: а)z=m(m>0) если m<c, если m=c, если m>c, m→∞ - полуоси эллипсов увеличиваются  b)y=0, действительная ось Oz, мнимая Ox y=n, n=b, n>b. Аналогично рассматривается сечения поверхности плоскостью х=0 и ей параллельными плоскостями. В пространстве между плоскостями z=c и z=-c –точек нет. Композиция двух аффинных преобразований есть аффинное преобразование плоскости (доказательство). Те-ма :Мн-во всех аффинных преобразований пространства Аn есть группа отн композиции преобразований. Пусть аффинное преобразование f пространства Аn переводит произвольную точку М (x1,x2,…,xn) в репере (О, е1,е2, ..., еn) (1) в точку М' (х'1,х'2,...,х'n) в том же репере, вычисляемыми по формулам Х'=АХ+АХ1(2). Пусть, далее, аффинное преобразование g пространства Аn переводит точку М' в точку М" с координатами x1``,x2``,…,xn`` (3) в репере (1). Тогда имеют место формулы: Х"=ВХ'+В1(4). где В — невырожденная матрица; X" — координатный столбец,
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 580. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Определение:Однополостным гиперболоидом называется множество всех точек пространства координаты которых в некотором специально выбранном ортонормированном репере удовлетворяет уравнению:
Определение:Однополостным гиперболоидом называется множество всех точек пространства координаты которых в некотором специально выбранном ортонормированном репере удовлетворяет уравнению:  ,
, -эллипс (горловой)
-эллипс (горловой)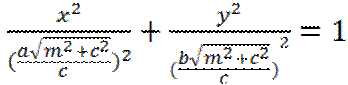
 -гипербола
-гипербола Определение:Двуполостным гиперболоидом называется множество всех точек пространства координаты которых в некотором специально выбранном ортонормированном репере удовлетворяет уравнению:
Определение:Двуполостным гиперболоидом называется множество всех точек пространства координаты которых в некотором специально выбранном ортонормированном репере удовлетворяет уравнению:  ,
,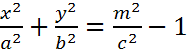 ,
, –мнимый эллипс
–мнимый эллипс –точка С1(0,0,с) и С2(0,0,-с)
–точка С1(0,0,с) и С2(0,0,-с)


 - гипербола
- гипербола n<b-гипербола(║Оz)
n<b-гипербола(║Оz)

 составленный из чисел (3); В1 — координатный столбец, составленный из некоторых чисел b1,b2,…,bn
составленный из чисел (3); В1 — координатный столбец, составленный из некоторых чисел b1,b2,…,bn  Р. Подставляя выражение X' из формулы (2) в (4), получаем Х"=(ВА)Х + (ВА1+В1). (5) Эти формулы выражают координаты точки М." в репере (1) через координаты точки М в том же репере, т. е., другими словами, они являются координатным выражением отображения gof:An An в репере (1). Это отображение является аффинным преобразованием пространства Аn. Итак, композиция двух аффинных преобразований пространства Аn есть аффинное преобразование пространства Аn. Т.е. композиция аффинных преобразований обладает свойством ассоциативности. Тождественное отображение е:Аn Аn задается формулой Х=ЕХ, где Е — единичная матрица, и поэтому является аффинным преобразованием, играющим роль нейтрального элемента. Из формулы (3) получаем X=A-1 X` - A-1A1. Эта формула является координатным выражением преобразования f-1:Аn Аn. Из нее видно, что f-1 — аффинное преобразование пространства Аn.
Р. Подставляя выражение X' из формулы (2) в (4), получаем Х"=(ВА)Х + (ВА1+В1). (5) Эти формулы выражают координаты точки М." в репере (1) через координаты точки М в том же репере, т. е., другими словами, они являются координатным выражением отображения gof:An An в репере (1). Это отображение является аффинным преобразованием пространства Аn. Итак, композиция двух аффинных преобразований пространства Аn есть аффинное преобразование пространства Аn. Т.е. композиция аффинных преобразований обладает свойством ассоциативности. Тождественное отображение е:Аn Аn задается формулой Х=ЕХ, где Е — единичная матрица, и поэтому является аффинным преобразованием, играющим роль нейтрального элемента. Из формулы (3) получаем X=A-1 X` - A-1A1. Эта формула является координатным выражением преобразования f-1:Аn Аn. Из нее видно, что f-1 — аффинное преобразование пространства Аn.