
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные св-ва аф.преобразований.1)При аф. пр. прямая отобр. в прямую (плоскость—в плоскость) 2) Аф.пр. сохраняет параллельность прямых и плоскостей. Док-во: d1: A1х+B1у+C1=0 найдем образы d2: A2х+B2у+C2=0 по аф.пр. d1//d2 A1/A2=B1/B2 ¹C1/C2 3)Аф.пр. плоскост (про-ства) сохр. Простое соотн. трех точек. Пусть аф преоб задано преходом от репера R к реперу R’. При этом образами А,В,С будут точки А’,В’,С’ . Тогда АВ=φBC следует A’B’=φB’C’ в силу коллинеарности векторов 4)Аф. пр. отрезок отобр. в отрезок, луч в луч, угол в угол. 5)Сущ. Единственное аф.пр., которое данную 3-ку точек О,А,В переводит в произвольную тройку точек этой же плоскости. 6)Аф. пр. опред. Реперами R{o,e1,e2} и R’{o’,e1’,e2’}. Пусть мн-во точек М(х,у) удовл. ур-ю F(х,у)=0 в R. Мн-во т.М(х,у) при аф.пр. отобрж. В мн-во т. М’(х,у) в R’ , которые удовл. Ур-ю F(х,у)=0 в R’.
Преобразовагие ве-ров при аф. пр. плоскости. Св-ва: 1) При аф. пр. в. u= MN переходит в u’= M’N’ , причем U’ имеет такие же корд. в R’ что и u в R . 2) Равным век-ром соотв. равные век-ры. 3)Век-ру u+v соотв. при аф. пр. в-р u’+v’ , а uv ,где u’ и v’ образы в-ров u и v при вф. пр. 4)Если при аф. пр. конечная сист-ма в-ров u1,u2,…un переходит соотв. u’1,u2’,…un’ то в-ру l u1, l u2,… l un 5) Аф. пр. сохр. лин. завис-мость век-ров. Док-во; Если сис-ма век-ров лин. зав. То их лин. комб-ей есть ноль век-р и $ кооф. Отличный от нуля.При аф.пр. лин.комб. век-ров переходит в лин.комб. их образов, тогда сохр. Их лин.завис-мость век-ров. 6) При аф.пр. всякая лин. незав. сис-ма в-ров переходит в лин.незав. сис-му в-ров. Док-во: Предположим что лин.незав. сис-ма в-ров при аф.пр. f переходит в л.з. сис-му. Тогда отоброжение f—1 есть обратное аф.пр. Тогда f—1 переводит сис-му в-ров в лин.зав. что противоречит условию.  7) Аф.пр. переводит репер в репер.
Центр линии второго порядка. Центральные и нецентральные линии. Определение: Точка С называется центром линий второго порядка, если для любой точки М принадлежащей этой линии, точка М1 будет симметрично точке М относительно точки С и тоже принадлежит линии.
Теорема: Точка М0(x0,y0) ,будет центром линий второго порядка тогда и только тогда, когда её координаты удовлетворяют системе уравнений:
Следствие: Рассмотрим условие зависимости которое определяет решение этой системы: Т.е. I2≠0, если линии эллиптического и гиперболического типа то эти линии имеют единственный центр эти линии называются центральными.
Эллипсоид, его сечения.
где a>0,b>0,c>0. Для исследования формы эллипсоида применим метод сечения, т.е. будем пересекать его плоскостями z=h, y=h, x=h h В пл-ти z=h возьмем декартову прямоуг. сист. координат O’x’y’. Начало кот. т. O’(0,0,h), а оси O’x’ и O’y’ сонаправ-ны в соответст. с осями Ox и Oy. В новой системе коор-т линия полученная в системе имеет уравнение:
1) |h|<c, если 2) |h|=c, тогда 3) |h|>c, тогда Определение:В случае, когда 2 полуоси эллипсоида равны – он назыв. эллипсоидом вращения, т.к. может быть получен вращением эллипса вокруг одной из его осей. Если a=b=c – сфера.
Конус. Конические сечения.
где a>0,b>0,c>0. Свойства: 1.Симетричность (относительно: координатных плоскостей, координатных осей и начало координат) 2.О(0,0,0) –вершина конуса 3.Основное свойство конуса: M0(x0,y0,z0)-принадлежит конусу, то все точки прямой OM0 лежат на конусе Докажем: OM0:
4.Форма конуса: а) z=m,m>0, m→∞ - полуоси эллипса увеличиваются b)x=0, пара пересекающихся прямых O(0,0,0) x=n, n>0 –гипербола Аналогично можно рассматривать сечения плоскостью y=k. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 262. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (*)
(*)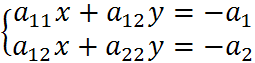 , система имеет единственное решение, если
, система имеет единственное решение, если  .
.
 Определение:Эллипсоидам называется множество всех точек пространства координаты которых в некотором специально выбранном ортонормированном репере удовлетворяет уравнению:
Определение:Эллипсоидам называется множество всех точек пространства координаты которых в некотором специально выбранном ортонормированном репере удовлетворяет уравнению:  ,
, R (плоскости
R (плоскости  осям). При конкретном h линии полученные в сечении опред. в прост-ве системой уравнений:
осям). При конкретном h линии полученные в сечении опред. в прост-ве системой уравнений: 

 , то
, то 
 , то (0,0,±с)
, то (0,0,±с) т-к пересечения не будет.
т-к пересечения не будет. Определение:Конусам второго порядка называется множество всех точек пространства координаты которых в некотором специально выбранном ортонормированном репере удовлетворяет уравнению:
Определение:Конусам второго порядка называется множество всех точек пространства координаты которых в некотором специально выбранном ортонормированном репере удовлетворяет уравнению:  ,
, , t€R
, t€R

 ,
, 