
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Аналитическое задание движений.Теорема 1. пусть дан частный случай аффинного преобразования : движение, которое определено двумя реперами R{O,i,j} R’{O’,i’j’}, тогда матрица данного преобразования является ортогональной. f: x’= c11x+ c12y+ x0 y’= c21x+c22y+ y0, Теорема 2. Если в ортонормированном репере афф преоб задано зависимостью x’= c11x+ c12y+ x0 y’= c21x+c22y+ y0,, где матрица С-ортогональна, то это преобразование является движением
17.Аналитическое задание аффинного преобразования. Теорема 1. Пусть заданы два репера на плоскости, которые определяют аффинные преобразования. Выполняются след условия е1’{c11;c12} e2’{c21 c22} ; O’(x0,y0) Пусть т М®M’, которая имеет координаты М’(x’,). Тогды веры след зависимости: x’= c11x+ c12y+ x0 y’= c21x+c22y+ y0, где матрица С-невырожденная Теорема 2 (обратная) Пусть заданы отображение плоскости на себя и некоторый репер R{O,i,j}, М®M’ так, что в репере R М’ имеет координаты: x’= c11x+ c12y+ x0 y’= c21x+c22y+ y0, где матрица С-невырожденная. Тогда данное отображение является аффинным. Теорема(общая) Пусть на плоскости задан репер R{O,i,j}, отображение плоскости в себя , при котором каждой точки М®M’, будет аффинным преобразованием тогда и только тогда , когда: x’= c11x+ c12y+ x0 y’= c21x+c22y+ y0, где матрица С-невырожденная Опр. Если определитель матрицы С>0, то аффин преобр называется ПЕРВОГО РОДА, если определитель С<0, то ВТОРОГО РОДА. Неподвижные точки и прямые при аффинных преобразованиях. Точка называется неподвижной точкой аффинного преобраз, если она переходит сама в себя при этом афф преобраз.Прямая называется неподвижной, если каждая ее точка неподвижна.
Основные виды движений плоскости.  Параллельный перенос на вектор a. Опр.Параллельным переносом наз.такое отобр.пл-ти на себя,при кот.любая т.M переходит в т.M’ так,что MM’=a,где a-з1аданный ненулевой вектор. Т-а.Параллельный перенос есть движение первого рода. Док-во. R={I,j,k}- орт репера Пусть a(a1,a2), M(x,y)→M’(x’,y’).MM’(x’-x,y’-y); Тогда x’-x=a1;y’-y=a2,т.е. x’=x+a1; y’=y+a2. C= ее определитель detC=1 Это движение первого рода Вращение вокруг точки. Опр.Пусть на пл-ти задана некоторая т.C и направленный угол φ,не равный 0.Поставим в соотв.т.M такую т.M’,что угол MCM’=φ,CM’=CM.Такое преобр. наз.вращением вокруг точки C. Точка С наз центром вращения, угол Р-углом поворота. M(x,y); M’(x’,y’)-ее образ; M(ρ,α); x=ρcosα; y=ρsinα. Тогда коорд.т.M’: x’=ρcos(φ+α)= ρcosφcosα-ρsinφsinα; y’= ρsin(φ+α)= ρsinφcosα+ρcosφsinα; или x’=cosφx-sinφy; y’=sinφx+cosφy. Рассм.случай,когда т.C не совпадает с нач.коорд. x’=cosφX-sinφY;y’=sinφX+cosφY.R’{C,i,j}.Подставляем Х=х-х0,Y=y-y0,X’=x-x0,Y’=y’-y0, X’=(x-x0)cosφ-(y-y0)sinφ; Y’=(x-x0)sinφ+(y-y0)cosφ; (x’-x0)=(x-x0)cosφ-(y-y0)sinφ; (y’-y0)=(x-x0)sinφ+(y-y0)cosφ; x’=cosφx-sinφy+x0+(-x0cosφ+y0sinφ); y’=sinφx+cosφy+y0+(-x0sinφ-y0cosφ). C= зн.данное отобр.явл.аф.преобр.первого рода, detC=1. Центральная симметрия. Опр.Пусть на пл-ти задана точка С. Отобр.пл-ти на себя,при кот.каждой т.M→M’,так что CM’=-CM наз.центральной симметрией.С-центр симметрии. Т-а.Центральная симметрия есть движение 1-ого рода. Док-во.C(x0,y0);M(x,y);M’(x’,y’);CM(x-x0,y-y0);CM’(x’-x0,y’-y0);x’-x0=-(x-x0);y’-y0=-(y-y0); x’=-x+2x0; С= y’=-y+2y0; Прямая,проход.через центр симметрии отобр.в себя,такая прямая наз.инвариантной,а неподвижная точка одна.Центральная симметрия-частный случай поворота(на 180 градусов). Осевая симметрия. Опр.Пусть на пл-ти задана некоторая прямая l.Отобр.пл-ти на себя,при кот.каждой т.M→M’,таким образом,что выполн.условия:1)MM’перпендикулярно l; 2)MM’ делится прямой l пополам. Т-a.Осевая симметрия есть движение второго рода. Д-во.Пусть прямая l совпадает с осью OX,тогда любой т. M→M’.M(x,y);M’(x,-y);x’=x;y’=-y.C= Прямая l явл.неподвижной прямой. Скользящая симметрия. Опр.Скользящей симметрией наз.композиция парал. переноса на вектор и осевой симметрии относ. прямой,парал.направлению переноса. Рассм.аналит.задание скользящей симм.Введём ортонорм.репер так,чтобы ось OX совпадала с заданной прямой m.Тогда вектор v(v1,0). x’=x+v1, y’=y-0 парал.перенос; x’’=x’, y’’=-y’-осев.симм. x’’=x+v1, y’’=-y. Матрица этого преобразования С=
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 329. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
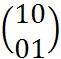 яв-ся ортогональной матрицей,
яв-ся ортогональной матрицей,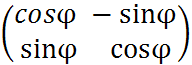 -матр.орт-льна,
-матр.орт-льна,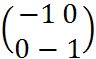 матрица ортогональна и detC=1
матрица ортогональна и detC=1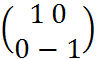 ,detC=-1/
,detC=-1/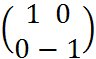 detC=-1-скользящая симметрия движение второго рода/
detC=-1-скользящая симметрия движение второго рода/