
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Рассмотрим прямоугольник со сторонами a и b и площадью S.2) Достроим прямоугольник до квадрата со стороной a + b, как показано на рисунке. Площадь квадрата равна квадрату его стороны, поэтому
3) Из рисунка видно, что квадрат составлен из двух прямоугольников со сторонами a и b и двух квадратов, причем один из них со стороной a имеет площадь a2, а второй – со стороной b имеет площадь b2. Следовательно, площадь каждого прямоугольника равна
Доказательство: Пусть дан прямоугольный треугольник Т со сторонами a и b. Достроим его до прямоугольника Р со сторонами a и b, проведя через вершины его острых углов прямые, перпендикулярные катетам. Гипотенуза треугольника разбивает прямоугольник на два равных треугольника Т и Т1. Поэтому
Теорема о площади произвольного треугольника. Площадь треугольника равна половине произведения любой из его сторон и проведенной к ней высоты: Доказательство: 1) Пусть D АВС – остроугольный, тогда BN ^ AC лежит внутри треугольника. 2) Пусть D АВС – тупоугольный с тупым углом С и BN ^ AC лежит внутри треугольника.
Доказательство:
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
Пусть Т – прямоугольный треугольник с катетами a и b и гипотенузой с. 2). Построим квадрат K со стороной a + b. На сторонах квадрата отметим точки D, E, F, G так, чтобы отрезки DE, EF, FG, GD отсекали от квадрата K прямоугольные треугольники Т1, Т2, Т3 и Т4 с катетами a и b.  3). Все прямоугольные треугольники Т1, Т2, Т3 и Т4 равны треугольнику Т (по двум катетам). Поэтому их гипотенузы равны гипотенузе треугольника Т. Следовательно DE = EF = FG = GD. Докажем, что четырехугольник DEFG является квадратом. По принципу равносоставленности Значение теоремы Пифагора. Это одна из главных теорем геометрии. С ее помощью можно вывести большинство теорем геометрии. Билет № 19. Признаки подобия прямоугольных треугольников. Доказать теорему о том, что в подобных треугольниках отношение двух соответствующих сторон равно отношению двух соответственных высот, биссектрис, медиан. Если в двух прямоугольных треугольниках острый угол одного равен острому углу другого, то такие треугольники подобны.
Если в двух прямоугольных треугольниках катеты одного треугольника пропорциональны катетам другого, то такие треугольники подобны.
Если в двух прямоугольных треугольниках гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого, то такие треугольники подобны.
DDBE = D А1В1С1 по гипотенузе и катету. DDBE ~ D АВС Þ D А1В1С1 ~ D АВС. Теорема об отношении сходственных отрезков в подобных треугольниках. В подобных треугольниках сходственные стороны пропорциональны сходственным высотам, сходственным биссектрисам, сходственным медианам.
Так как DABC~DA1B1C1, то ÐA =ÐA1 и ÐВ =ÐВ1. ÐABD =ÐA1B1D1=0,5ÐВ по свойству биссектрисы Þ
Так как DABC~DA1B1C1, то ÐA =ÐA1, |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 290. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 Теорема о площади прямоугольного треугольника. Площадь прямоугольного треугольника равна половине произведения его катетов.
Теорема о площади прямоугольного треугольника. Площадь прямоугольного треугольника равна половине произведения его катетов.



 Вычисление площади треугольника через угол. Площадь треугольника равна половине произведения его сторон и синуса угла между ними:
Вычисление площади треугольника через угол. Площадь треугольника равна половине произведения его сторон и синуса угла между ними:

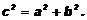
 Доказательство:
Доказательство: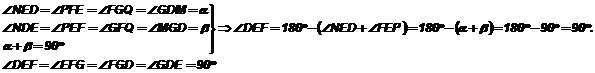
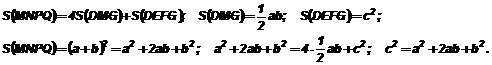
 Следствие первого признака подобия: ÐС =ÐС1 = 90°; ÐА = ÐА1.
Следствие первого признака подобия: ÐС =ÐС1 = 90°; ÐА = ÐА1.
 Пусть АВС и А1В1С1 – два треугольника с прямыми углами С и С1 и
Пусть АВС и А1В1С1 – два треугольника с прямыми углами С и С1 и  На стороне АС DАВС отложим отрезок AD = A1C1 от точки С и проведем DE II AB. Получим вспомогательный DDBE~DABC. Из подобия треугольников следует:
На стороне АС DАВС отложим отрезок AD = A1C1 от точки С и проведем DE II AB. Получим вспомогательный DDBE~DABC. Из подобия треугольников следует:  Сравнивая эту пропорцию с данной по условию, получим:
Сравнивая эту пропорцию с данной по условию, получим:  Отсюда следует, что DE = A1C1.
Отсюда следует, что DE = A1C1.  Так как DABC~DA1B1C1, то ÐA =ÐA1. DABD~DA1B1D1, так как ÐA =ÐA1 и ÐАDB = ÐА1D1B1.
Так как DABC~DA1B1C1, то ÐA =ÐA1. DABD~DA1B1D1, так как ÐA =ÐA1 и ÐАDB = ÐА1D1B1.

 по свойству медиан. DABD~DA1B1D1, так как ÐA =ÐA1 и
по свойству медиан. DABD~DA1B1D1, так как ÐA =ÐA1 и  Þ
Þ