Теорема 2 (о существовании описанной окружности): Около любого  треугольника можно описать окружность и притом только одну.

Дано: DАВС. Доказать:

1). Существование описанной окружности с центром в точке О.

2) Единственность такой окружности.

Доказательство:

1. В произвольном треугольнике АВС обозначим буквой О  точку пересечения серединных перпендикуляров, так как все серединные перпендикуляры в треугольнике пересекаются в одной точке. Соединим точку O с вершинами треугольника. Отрезки AO = ВO = CO, так как точка O  равноудалена от вершин треугольника. Поэтому окружность с центром в точке O проходит через все вершины треугольника АВС и является описанной около треугольника. 2. Допустим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки O до вершин треугольника. Следовательно, эти окружности совпадают.

Определение 2. Треугольник называется описанным около окружности, а окружность – вписанной в треугольник, если все стороны треугольника лежат на касательных к окружности.

Теорема 3 (о центре вписанной окружности). Биссектрисы треугольника пересекаются в одной точке.

Дано: D АВС; АА₁, ВВ₁, СС₁ - биссектрисы.

Доказать: АА₁ ∩ ВВ₁ = {O};  АА₁ ∩ СС₁ = {O}.

Доказательство:

1. Пусть биссектрисы АА₁ и ВВ₁ пересекаются в точке О. Построим из точки О перпендикуляры OK, ON и OP к сторонам АВ, ВС и АС треугольника.

2. По характерному свойству биссектрисы ОК = ОР, так как точка О лежит на биссектрисе   АА₁; и OK = ON, так как точка О лежит на биссектрисе ВВ₁. Следовательно, ОК = ОР = ON.

3. Если ОР = ON, то точка О равноудалена от сторон угла С и лежит на биссектрисе СС₁. 

Вывод: Точка пересечения биссектрис треугольника равноудалена от всех его сторон и является центром вписанной окружности. Точка пересечения биссектрис треугольника называется инцентром.

Теорема 4 (о существовании вписанной окружности): В любой треугольник можно вписать окружность и притом только одну.

Дано: DАВС. Доказать:

1). Существование вписанной окружности с центром в точке О.

2) Единственность такой окружности.

Доказательство:

1. В произвольном треугольнике АВС обозначим буквой О  точку пересечения биссектрис, так как все биссектрисы в треугольнике  пересекаются в одной точке. Опустим из точки O перпендикуляры на все стороны треугольника. Так как точка О равноудалена от сторон треугольника, то отрезки OK = ON = OP. Поэтому окружность с центром в точке O касается всех сторон треугольника АВС и является вписанной в него.

2. Допустим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от сторон треугольника и поэтому совпадает с точкой пересечения биссектрис углов треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают.

2.  Доказать теорему синусов. Следствие. 

Теорема синусов. Отношение двух сторон треугольника равно отношению синусов противолежащих им углов.

Доказательство: 

Проведем из точки В перпендикуляр к стороне АС.

2). Из DABD (ÐADB = 90°): BD = AB∙sinA.

3). Из DBCD (ÐBDC = 90°): BD = BC∙sinC. 

4). AB∙sinA = BC∙sinC. 

Теорему синусов можно сформулировать и так: синусы углов треугольника пропорциональны противолежащим сторонам.

Теорема  синусов  традиционно  выводится  из  равенства  трех  выражений  площади  треугольника.  Однако  ее  можно  получить  совсем просто  и  в  ее  полном  содержании  без  использования  формулы  площади.

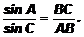
Проведем  радиус  OD  окружности,  описанной около  данного  треугольника  ABC,  перпендикулярный  к  стороне  BC.  Тогда  углы BAC  и  BOD равны,  так  как  оба  измеряются  половиной  дуги BC.  Точка  E  пересечения  BC  и  OD — середина BC.  Поэтому  из  прямоугольного DВОЕ имеем: