
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
CD пересекает окружность.При первом предположении построим какую-нибудь касательную C1D1 к окружности, не пересекающую отрезок CD. Тогда по необходимому условию для описанного четырехугольника ABC1D1 имеем: AB + C1D1 = BC1 + AD1. Но т. к. BC1 = BC − CC1, AD1 = AD − DD1, то AB + C1D1 = BC − CC1 + AD − DD1, откуда C1D1 + CC1 + DD1 = BC + AD − AB. Из условия AB + CD = BC + AD следует BC + AD − AB = CD. Следовательно, C1D1 +CC1 +DD1 =CD. Оказалось, что в четырехугольнике CC1D1D одна сторона равна сумме трех других, что невозможно. Аналогично опровергается второе предположение. Теорема доказана.
Доказательство: По свойству касательных, проведенных к окружности из одной точки: AN = AP, BP = BT, CN = CT = r. AC = AN + r, BC = BT + r, AB = AP + PB. AC + BC = AN + BT + 2r = AB + 2r. a + b =c + 2r.
2. Доказать теорему о точке пересечения медиан треугольника. Теорема о свойстве медиан треугольника. Три медианы пересекаются в одной точке. Эта точка делит каждую из медиан в отношении 2:1, считая от вершины.
1). Медиана АА1 пересекает АВ в точке А1. Медиана ВВ1 пересекает АС в точке В1. Тогда А1В1– средняя линия. 2). Рассмотрим D АОВ и D А1ОВ1.
3). Из подобия треугольников:
4). Аналогично доказывается, что точка О делит медиану СС1 в отношении 2:1. Билет № 16. Подобные треугольники. Доказать теорему о прямой, параллельной стороне треугольника и пересекающей две другие его стороны. В повседневной жизни часто встречаются тела и фигуры одинаковой формы, но разных размеров. В геометрии фигуры одинаковой формы принято называть подобными. 
Определение подобных треугольников. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника. Иначе: Число k, равное отношению сходственных сторон, называется коэффициентом подобия.
Доказательство: Рассмотрим DАВС и DА1ВС1.
Доказать теорему о сумме квадратов диагоналей параллелограмма. Теорема. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
ABCD – параллелограмм; AC ∩ BD = {O}. Доказать:
Доказательство: Рассмотрим DBAD. По теореме косинусов: Рассмотрим DABC. По теореме косинусов: 3. По свойству углов, прилежащих к одной стороне параллелограмма: ÐBAD + ÐABC = 180° Þ a + b = 180°° Þ b = 180° − a. 4. Преобразуем выражение для стороны AC, используя формулы приведения: Найдем сумму квадратов отрезков АС и ВD, являющихся диагоналями параллелограмма ABCD.
Поскольку по свойству параллелограмма BC = AD, то
Билет № 17. Четыре замечательных точки треугольника. Доказать теоремы о центре тяжести и ортоцентре треугольника. Замечательными точками треугольника являются: Точка пересечения биссектрис треугольника. Она равноудалена от всех его сторон и является центром вписанной окружности. Точка пересечения биссектрис треугольника называется инцентром. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 256. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Теорема о сумме катетов прямоугольного треугольника. Сумма катетов прямоугольного треугольника равна разности гипотенузы и диаметра вписанной окружности.
Теорема о сумме катетов прямоугольного треугольника. Сумма катетов прямоугольного треугольника равна разности гипотенузы и диаметра вписанной окружности.
 Доказательство:
Доказательство: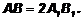


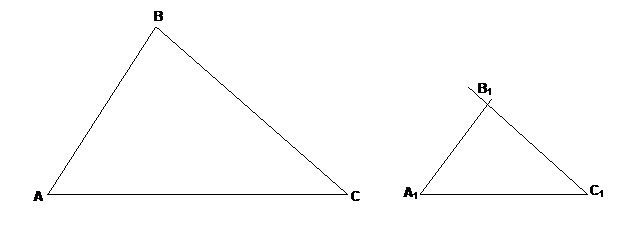 Рассмотрим подобные треугольники АВС и А1В1С1. У них углы соответственно равны и называются соответственными: ÐА = ÐА1; ÐВ = ÐВ1; ÐС = ÐС1. Стороны, лежащие против равных углов, называются сходственными: АВ и А1В1; ВС и В1С1; АС и А1С1.
Рассмотрим подобные треугольники АВС и А1В1С1. У них углы соответственно равны и называются соответственными: ÐА = ÐА1; ÐВ = ÐВ1; ÐС = ÐС1. Стороны, лежащие против равных углов, называются сходственными: АВ и А1В1; ВС и В1С1; АС и А1С1. 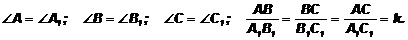
 Следствие первого признака подобия. Прямая, параллельная какой-либо из сторон треугольника, отсекает от него треугольник, подобный исходному.
Следствие первого признака подобия. Прямая, параллельная какой-либо из сторон треугольника, отсекает от него треугольник, подобный исходному.
 Дано:
Дано:
 где ÐBАD = a.
где ÐBАD = a. где ÐABC = b.
где ÐABC = b. так как по формуле приведения
так как по формуле приведения  поскольку ÐABC = 180°−a находится во второй четверти.
поскольку ÐABC = 180°−a находится во второй четверти.
