
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Где R — радиус описанной окружности.Аналогично b = 2RsinB и c = 2RsinC. Отсюда Нетрудно проверить, что в случае, когда угол A тупой или прямой, результат будет тот же. Для практического применения теорему синусов полезно знать и в такой формулировке: каждая Сторона треугольника равна диаметру описанной около него окружности, умноженному на синус угла, противолежащего этой стороне. В доказательствах некоторых соотношений при выполнении тождественных преобразований теорему синусов можно использовать в виде: asinB = bsinA, bsinC = csinB, csinA = asinC.
Билет № 14. Доказать теорему о четырехугольнике, вписанном в окружность, и теорему, ей обратную. Так как центр описанной около четырехугольника окружности равноудален от его вершин, то он принадлежит серединным перпендикулярaм к его сторонам и диагоналям. Обратно, если серединные перпендикуляры к трем сторонам четырехугольника пересекаются в одной точке, то эта точка будет равноудалена от всех его вершин и поэтому будет центром описанной около него окружности. Итак, для того, чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы серединные перпендикуляры к трем его сторонам пересекались в одной точке. Другой критерий вписанного четырехугольника связан с его углами.
 Необходимость этого условия очевидна: сумма углов A и C вписанного четырехугольника ABCD измеряется полусуммой дуг BCD и BAD, составляющих полную окружность, и потому равна 180°. Доказательство: По теореме о градусной мере вписанного угла в окружности Теорема (обратная). Если сумма противоположных углов четырехугольника равна 180°, то около него можно описать окружность.
предположения: Точка C находится вне окружности, Она лежит внутри окружности. При первом предположении и усло- вии ∠A > 90° стороны BC и DC пересекают окружность вторично в своих внутренних точках E и F. Тогда для вписанного четырехугольника ABED по необходимому условию будет ∠A+∠BED=180°. По теореме о внешнем угле треугольника ∠BED > ∠C и потому ∠A+∠C < 180°, что противоречит условию. Второе предположение аналогично приводит к противоречию ∠A + ∠C > 180°. Доказательство закончено. Доказательство: 1) Проведем окружность через три вершины четырехугольника A, B, D и докажем, что она проходит также через вершину С. Пусть это не так. Тогда вершина С лежит либо вне круга, либо внутри круга. Пусть точка С лежит вне круга. Тогда Это противоречит условию теоремы. Следовательно, точка С не может лежать вне окружности.
Пусть точка С лежит внутри круга. Тогда Это противоречит условию теоремы. Следовательно, точка С не может лежать внутри окружности. Вывод: Чтобы выполнялось условие теоремы, точка С должна лежать только на окружности, а четырехугольник ABCD должен быть вписанным в окружность. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 256. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 Теорема. Для того, чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы сумма его противоположных углов была равна 180° (т. е. суммы его противоположных углов были равны).
Теорема. Для того, чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы сумма его противоположных углов была равна 180° (т. е. суммы его противоположных углов были равны).
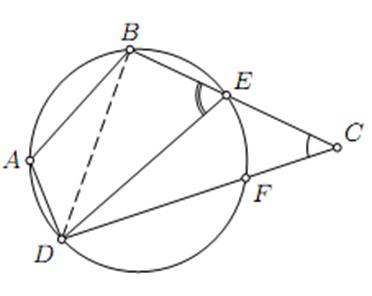 Достаточность. Пусть ∠A + ∠C = 180◦. Тогда эти углы не могут быть оба острыми или оба тупыми. Для определенности будем считать, что ∠A > 90◦. Опишем около треугольника ABD окружность и докажем, что точка C ей принадлежит. Для этого необходимо опровергнуть два возможных
Достаточность. Пусть ∠A + ∠C = 180◦. Тогда эти углы не могут быть оба острыми или оба тупыми. Для определенности будем считать, что ∠A > 90◦. Опишем около треугольника ABD окружность и докажем, что точка C ей принадлежит. Для этого необходимо опровергнуть два возможных



