
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метричні задачі на пряму і площинуМетричні задачі розглядаються в прямокутній системі координат. 1. Знаходження кута між двома прямими у просторі. Кутом між прямими називається мінімальний кут між їх направляючими векторами. Нехай прямі мають направляючі вектори
Сам кут знайдемо як арккосинус отриманого числа (враховуючи, що кут гострий). Звідси одразу випливає умова перпендикулярності двох прямих: 2. Кут між прямою і площиною Кутом між прямою і площиною наз. гострий кут між прямою і її проекцією на площину.
Косинус кута між векторами знаходимо із скалярного добутку:
3.Відстань від точки до прямої у просторі:
Відкладемо вектор Розглянемо паралелограм М1М0Q0Q1. Ясно, що відстань d від т.М0 до даної прямої а дорівнює висоті паралелограма М1М0Q0Q1, яку обчислимо, розділивши площу паралелограма на довжину сторони М1Q1, тобто на модуль вектора  S=d | Тоді Перейшовши до координат, отримаємо: d = Відмітимо, що відстань d можна знайти і як відстань між двома точками: точкою М0 і її ортогональною проекцією на дану пряму (див. приклад 50). 4.Відстань між мимобіжними прямими.
Отже, V=S× d=|[ Звідки d= Відмітимо, що відстань між мимобіжними прямими можна знайти й іншим способом, наприклад, як відстань від будь-якої точки однієї прямої до площини, яка проходить через другу пряму, паралельно до першої. Р-ня такої площини отримаємо за двома направляючими векторами і точкою (направляючими векторами площини будуть направляючі вектори даних прямих).
Еліпс Еліпсом наз. множина всіх точок площини координати яких, в деякій прямокутній с-мі корд., задовольняють р-ня: З р-ня еліпса маємо: Так як змінні в р-ня еліпса входять лише в другій степені, то еліпс симетричний відносно координатних осей і початку системи координат. Відмітимо елементи еліпса, які не залежать від орієнтації координатних осей: 1. 2. число b – мала піввісь (2b – мала вісь), 3. 2c – фокальна відстань (c2=a2-b2), 4. e = 5. точка О(0,0) – центр еліпса, 6. А1(а,0), А2(-а,0), В1(0,b), В2(0,-b) – вершини еліпса, 7. Точки F1(с,0) , F2(-с,0) наз. фокусами, 8. прямі d1 i d2, які мають рівняння: x= Розгл. довільну т.М, яка належить еліпсу. Відрізки, які сполучають її з фокусами наз. фокальними радіусами т.М (довжини цих відрізків також наз. фокальними радіусами т.М). Нехай т.М еліпса має координати x, y. Тоді ÷ MF2÷ = = Аналогічно міркуючи, отримаємо: ÷ MF1÷ =÷ -ex+a÷. Так як для всіх точок еліпса ex < a ,то модулі приймають лише додатні значення, тому: ÷ MF1÷= -ex+a , ÷ MF2÷= ex+a . Тоді÷ MF1÷ +÷ MF2÷ =2a . Отже, ми отримали геометричне означення еліпса: Еліпсом наз. множина всіх точок площини сума відстаней від яких до двох даних точок (фокусів) є величина постійна (рівна 2а). Параметричні рівняння еліпса. Нехай задано еліпс канонічним рівнянням: Побуд. в прямокут. с-мі коор. два концентричні кола радіус. a і b, a>b (рис.9). Проведемо промінь ОК . Нехай він утворює з віссю ОХ кут φ. Точки перетину променя з колами позначимо N i Q. Проведемо через точку N пряму паралельну до oсі OX, а через Q пряму паралельну до OY. В перетині цих прямих отримаємо т.M(x, y). Тоді x=a cos φ, y=b sin φ . Покажемо, що т.M(acos φ, bsin φ) належить еліпсу. Дійсно, її координати задовольняють р-ня: Таким чином ми отримали параметричні рівняння еліпса:
y=b sinφ , де φ – параметр (0 Гіпербола. Гіперболоюназ. множина всіх точок площини координати яких, в деякій прямокутній с-мі коор., задовольняють р-ня: З р-ня гіперболи маємо: Отже, між прямими x = a і x = – a немає точок гіперболи. Так як в р-ня гіперболи входять тільки змінні парної степені, то гіпербола симетрична відносно осей OX, OY і початку с-ми коор. Ясно, що інших осей симетрії гіпербола не має, так як будь-яка вісь її симетрії проходить через т.О, а значить являється і віссю симетрії кола x2+y2=a2 , яке має з гіперболою дві спільні точки А1(а,0) та А2(-а,0); тому будь-яка вісь симетрії переводить А1 в А2 і навпаки, або залишає їх нерухомими. А це лише прямі OX і OY. При побудові гіперболи досить побудувати її у першій координатній четверті, а в інших – по симетрії. З р-ня гіперболи маємо: Таким чином, гіперболу можна побуд. за допомогою прямокутника із сторонами 2a і 2b, його діагоналі будуть асимптотами (рис.12). Основні елементи гіперболи, які не залежать від орієнтації системи координат: 1. а – дійсна піввісь; 2а – дійсна вісь. 2. b – уявна піввісь; 2b – уявна вісь. 3. 2c – фокальна відстань (c2=a2+b2). 4. 5. Точки А1(а,0) та А2(-а,0)– вершини гіперболи. 6. Точка О(0,0) – центр гіперболи. 7. Точки F1(c,0) і F2(-c,0) – фокуси гіперболи. 8. Прямі d1 і d2 : 9. Прямі Відрізки, які сполучають довільну точку гіперболи з фокусами, наз. фокальними радіусами. Як і для еліпса знайдемо:÷ MF1÷ =÷ex – a÷, ÷ MF2÷ =÷ex + a÷ Але так як для гіперболи ÷ex÷>÷x÷>a то ÷ MF1÷ –÷ MF2÷ = Одержали геометрич. озна.: гіперболою наз. множина всіх точок площини, модуль різниці відстаней від яких, до двох даних точок F1 і F2 (фокусів) є величина постійна (рівна 2а). Відмітимо, що у випадку a=b гіпербола наз. рівносторонньою. Теор9. Якщо за вісі прямокутної с-ми коор. взяти асимптоти рівносторонньої гіперболи, то в цій с-мі коор. гіпербола являє собою графік оберненої пропорційності Якщо Парабола. Параболою наз. множина всіх точок площини, координати яких, в деякій прямокутній с-мі коор. задовольняють р-ня: Так як у р-ні параболи в парній степені лише ордината, то парабола симетрична тільки відносно вісі OX і розміщена в першій і четвертій чвертях, якщо р>0 (рис.13) і другій та третій, якщо р<0. Вісь симетрії параболи наз. віссю параболи. Парабола проходить через т.О(0,0), яка наз. вершиною параболи. Інших точок перетину з осями координат парабола не має, тому вісь OX – єдина вісь симетрії параболи. Нехай р>0, тоді якщо x®¥ тоі y®¥ (рис.13).
1. число р – фокальний параметр. 2. число 3. точка F( 4. пряма d: Теор10.Парабола – це множина тих і тільки тих точок площини, які рівновіддалені від фокуса і директриси. Доведення. Нехай точка M(x,y) рівновіддалена від F і d. Умова рівновіддаленості: Навпаки, нехай т.М належить параболі, яка має р-ня Знайдемо відстань від т.М до фокуса:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 607. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 1 = (α1,β1,γ1), і
1 = (α1,β1,γ1), і 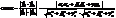 (46).
(46). 1×
1× 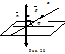 Познач. цей кут – j (рис.28). Нехай пряма а має направляюч. вектор
Познач. цей кут – j (рис.28). Нехай пряма а має направляюч. вектор  =(А,В,С) і направляючим вектором прямої = 900– j; або 900+j, якщо нормальний вектор направлений вниз (рис.28).
=(А,В,С) і направляючим вектором прямої = 900– j; або 900+j, якщо нормальний вектор направлений вниз (рис.28).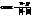 . Враховуючи, що сos(900– φ) = sinφ, сos(900+j) = – sinφ, маємо sinj = |cosa|. Отже, ми отримали ф-лу для знаходження синуса кута між прямою і площиною:
. Враховуючи, що сos(900– φ) = sinφ, сos(900+j) = – sinφ, маємо sinj = |cosa|. Отже, ми отримали ф-лу для знаходження синуса кута між прямою і площиною: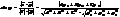 (47)
(47)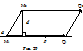 Нехай пряма а задана точкою М1(x1,y1,z1) і направляючим вектором
Нехай пряма а задана точкою М1(x1,y1,z1) і направляючим вектором 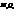 =
= 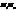 ]|. Знайдемо координати вектора
]|. Знайдемо координати вектора 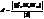 .
.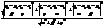 (48)
(48)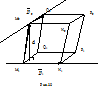 Розглянемо мимобіжні прямі а1, яка проходить через т.М1(x1,y1,z1), і має направляючий вектор
Розглянемо мимобіжні прямі а1, яка проходить через т.М1(x1,y1,z1), і має направляючий вектор  2 від т.М1, тоді вектор
2 від т.М1, тоді вектор 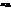 =
= 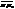 . Згідно теор12, об’єм цього паралелепіпеда рівний модулю змішаного добутку векторів
. Згідно теор12, об’єм цього паралелепіпеда рівний модулю змішаного добутку векторів 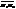 : V=|(
: V=|( 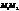 )|.
)|.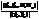 (49)
(49)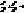 (14) де а ³ b>0.
(14) де а ³ b>0.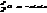 , аналогічно
, аналогічно 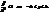 Отже, еліпс – це фігура обмежена прямокутником із сторонами 2а і 2b.
Отже, еліпс – це фігура обмежена прямокутником із сторонами 2а і 2b.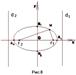 число а – велика піввісь (2а –велика вісь),
число а – велика піввісь (2а –велика вісь), – ексцентриситет (0<e<1),
– ексцентриситет (0<e<1),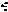 , наз. директрисамиеліпса (не мають спільних точок з еліпсом).
, наз. директрисамиеліпса (не мають спільних точок з еліпсом).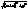 . Так як т.М належить еліпсу, то її координати задовольняють р-ня еліпса:
. Так як т.М належить еліпсу, то її координати задовольняють р-ня еліпса: 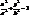 , звідки y2=b2(1–
, звідки y2=b2(1– 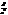 ). Отже,÷ MF2÷ =
). Отже,÷ MF2÷ = 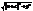 =
= 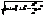 =
=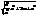 = =
= = 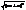 =÷ ex+a÷.
=÷ ex+a÷.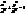
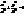 , отже вона належить еліпсу.
, отже вона належить еліпсу.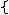 x=a cosφ ,
x=a cosφ , φ <2p ).
φ <2p ).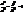 (15)
(15)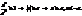
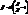 , або
, або 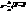 . Графік цієї функції необмежений і при х
. Графік цієї функції необмежений і при х 
 , наближається у першій четверті до прямої
, наближається у першій четверті до прямої 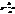 , яку наз. асимптотою гіперболи.
, яку наз. асимптотою гіперболи.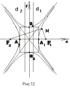 e =
e =  >1 – ексцентриситет.
>1 – ексцентриситет.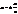 – директриси гіперболи.
– директриси гіперболи.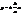 – асимптоти гіперболи
– асимптоти гіперболи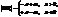 , і
, і 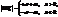 Звідси випливає, що
Звідси випливає, що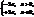 або ÷÷ MF1÷ –÷ MF2÷÷=2a .
або ÷÷ MF1÷ –÷ MF2÷÷=2a .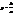 .
.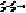 , то ми отримаємо гіперболу, яка наз. спряженою з
, то ми отримаємо гіперболу, яка наз. спряженою з 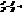 . Вона має ті ж асимптоти, але її фокуси лежать на вісі OY (рис.12).
. Вона має ті ж асимптоти, але її фокуси лежать на вісі OY (рис.12).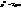 (16)
(16) Відмітимо основні елементи параболи, які не залежать від орієнтації системи координат:
Відмітимо основні елементи параболи, які не залежать від орієнтації системи координат: – фокальна відстань.
– фокальна відстань.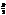 ,0) – фокус.
,0) – фокус.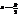 – директриса.
– директриса.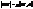 .
. 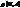 =÷ x+
=÷ x+ 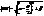 отже,
отже, 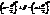 , або
, або 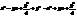 .Звідки
.Звідки 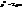 . Отже, якщо точка рівновіддалена від фокуса і директриси, то вона належить параболі (рис.13).
. Отже, якщо точка рівновіддалена від фокуса і директриси, то вона належить параболі (рис.13).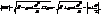 а це і є відстань від точки М до директриси.
а це і є відстань від точки М до директриси.