
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Рівняння площини в афінній системі координатВектор, який лежить на площині або паралельний до неї, наз. направляючим вектором площини. Площину в афінній с-мі коор. (О, 1.Рівняння площини, заданої двома направляючими векторами і точкою. Нехай площина π задана неколінеарними направляючими векторами
2. Рівняння площини, заданої трьома точками. Нехай площина задана трьома точками, які не лежать на одній прямій М1(x1,y1,z1), М2(x2,y2,z2), М3(x3,y3,z3). Тоді можна скористатися рівнянням (33), поклавши
3. Рівняння площини у відрізках (на осях): Нехай площина відтинає на осях координат відрізки a, b і c відповідно. Тоді вона проходить через точки А(а,0,0), В(0,b,0) і С(0,0,с). Використавши р-ня (34), маємо: Відмітимо, що a, b і c направлені відрізки, тому вони можуть бути і від’ємні. 4.Параметричні рівняння площини: Нехай площина π задана направляючими векторами x-x0=λα1+μα2 x=λα1+μα2+x0,  y-y0=λβ1+μβ2, або y=λβ1+μβ2+y0, (36) z-z0=λγ1+μγ2, z=λγ1+μγ2+z0, де λ, μ параметри (λ,μ 5. Загальне рівняння площини: Всі отримані нами рівняння площини – це рівняння першого степеня з трьома змінними, а тому їх можна записати загальним рівнянням Ax+By+Cz+D=0. (37) Теор16. Множина точок простору, координати яких в афінній с-мі коор. задовольняють р-ня (37), де А, В і С не рівні нулю одночасно, являє собою площину, причому Доведення: Розглянемо р-ня (37), де А, В і С Площина в прямокутній системі координат Так як прямокутна с-ма коор. (O, Нормальнимвектором площини наз. будь-який вектор, перпендикулярний до цієї площини. У прямокутній с-мі коор. можна отримати ще два р-ня площини: за точкою і нормальним вектором, та нормальне р-ня. 6.Рівняння площини за точкою і нормальним вектором. Нехай в прямокутній с-мі коор. (O, 7. Нормальне рівняння площини. Нехай площина задана в прямокутній с-мі коор. одиничним нормальним вектором x cosa1+y cosa2+z cosa3 –r =0 (39). |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 537. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  ,
,  ) можна задати двома направляючими векторами (неколінеарними)і точкою, або трьома точками, які не лежать на одній прямій.
) можна задати двома направляючими векторами (неколінеарними)і точкою, або трьома точками, які не лежать на одній прямій. =(α1,β1,γ1) і
=(α1,β1,γ1) і  =(α2,β2,γ2), та точкою М0(x0,y0,z0). Виберемо на площині ще одну довільну точку М(x,y,z). Розглянемо вектор
=(α2,β2,γ2), та точкою М0(x0,y0,z0). Виберемо на площині ще одну довільну точку М(x,y,z). Розглянемо вектор 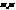 =(x-x0, y-y0, z-z0). Оскільки т.М належить площині то вектори
=(x-x0, y-y0, z-z0). Оскільки т.М належить площині то вектори 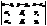 =0 (33)
=0 (33) =
= 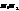 ,
,  =
= 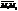 , а М0=М1. Отримаємо:
, а М0=М1. Отримаємо: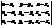 = 0 (34)
= 0 (34)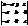 =0, або після елементарних перетворень:
=0, або після елементарних перетворень: 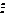 +
+ 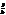 +
+  =1. (35)
=1. (35) R).
R). 0 одночасно. Його можна записати у вигляді:
0 одночасно. Його можна записати у вигляді: 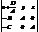 = 0. Отже, р-ня (37) рівносильне р-ню площини вигляду (33), заданої 2ма направляюч. векторами
= 0. Отже, р-ня (37) рівносильне р-ню площини вигляду (33), заданої 2ма направляюч. векторами  =(-В,А,0),
=(-В,А,0), 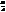 ;0;0).
;0;0). ,
,  ,
,  ) є частковим випадком афінної, то в ній можна використовувати всі отримані раніше р-ня (33)–(37) площини.
) є частковим випадком афінної, то в ній можна використовувати всі отримані раніше р-ня (33)–(37) площини. =(А,В,С). Візьмемо на площині довільну точку Н(x,y,z). Тоді
=(А,В,С). Візьмемо на площині довільну точку Н(x,y,z). Тоді 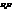 =(x-x0, y-y0, z-z0). Так як вектор
=(x-x0, y-y0, z-z0). Так як вектор 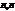 перпендикулярний до вектора
перпендикулярний до вектора  і відстанню r від початку координат до площини. Нехай Н – основа перпендикуляра, опущеного із початку координат на площину. Знайдемо координати т.Н. Так як координатами точки назвали координати її радіус-вектора, то знайдемо координати вектора
і відстанню r від початку координат до площини. Нехай Н – основа перпендикуляра, опущеного із початку координат на площину. Знайдемо координати т.Н. Так як координатами точки назвали координати її радіус-вектора, то знайдемо координати вектора  . Отже, координати точки Н (r cosa1, r cosa2, r cosa3). Використавши р-ня (38), отримаємо нормальне р-ня: cosa1(x-rcosa1)+cosa2(y-rcosa2)+cosa3(z-rcosa3)=0 або
. Отже, координати точки Н (r cosa1, r cosa2, r cosa3). Використавши р-ня (38), отримаємо нормальне р-ня: cosa1(x-rcosa1)+cosa2(y-rcosa2)+cosa3(z-rcosa3)=0 або