
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Еліпсоїд, гіперболоїди, параболоїди. Дослідження їх форм методом перерізів, їх побудова.Еліпсоїдомназ. поверхня, яка в деякій прямок.й с-мі коор. визначається р-ням: Дослідимо форму еліпсоїда і побуд. його: 1.Так як x, y, z, входять в р-ня (22) тільки в парних степенях, то еліпсоїд симетрич. відносно коор. площин, осей і почат. координат. Центр симетрії еліпсоїда наз. центром еліпсоїда, а вісі симетрії – його осями. Точки перетину еліпсоїда з осями координат: А1(а,0,0); А2(-а,0,0); В1(0,b,0); В2(0,-b,0); С1(0,0,с); С2(0,0,-с) наз. вершинами еліпсоїда. 2.Із р-ня (1) маємо: 3.Розг. перерізи еліпсоїда координат. площинами і площинами, || до них. Площина XOY і паралельні до неї площини мають р-ня z=h. В перетині еліпсоїда з такими площинами отримаємо Можливі три випадки: 1). ú h÷ < c, тоді маємо 2). ú h÷ = c, то одержуємо 3). ÷ h÷ > c, то одержуємо рівняння уявного еліпса, отже в цьому випад. площина z=h з еліпсоїдом не має спільних точок. Повністю аналогічно розглядаються перерізи еліпсоїда площинами x=h і y=h . Побудувавши еліпси в координатних площинах, отримаємо зображення еліпсоїда (рис.19). Відмітимо, що якщо в р-ні (22) а,b,с – різні, то еліпсоїд наз. трьохвісним, а якщо які-небудь дві із півосей рівні, наприклад а=с, то в перетині з площинами y=h, де ú h÷ < b, отримаємо кола (рис.20).  В цьому випадку еліпсоїд можна одержати обертанням еліпса Однопорожнинним гіперболоїдом наз. поверхня, яка в деякій прямокутній с-мі коор. визначається р-ням: Оскільки змінні входять в р-ня (24) тільки в парних степенях, то однопорожнинний гіперболоїд симетричний відносно всіх координатних площин, осей і початку с-ми коор. Дві вісі OX і OY перетин. Одно порожнин. гіперболоїд. Вони наз. дійсними, а вісь OZ не перетинає його, тому наз. уявною. Точки перетину поверхні з координатними осями наз. вершинами. Дослід. форму одно порожнин. гіперболоїда методом перерізів і побуд. його. 1). Розгул. перерізи одно порожнин. гіперболоїда площиною YOZ і || до неї площинами. Їх р-ня x=k. В перетині отрим.:
Можливі три випадки: а) якщо ÷ k÷ < a то маємо гіперболу з асимптотами b) якщо ÷ k÷ = a – одержуємо пару прямих, що перетинаються, c) якщо ÷ k÷ > a – одержуємо гіперболу з дійсною віссю, яка || до вісі OZ). Якщо k=0 – одержуємо гіперболу в площині YOZ, яку і будуємо (рис. 22). 2). Повністю аналогічні до попереднього перерізи отримуються в перетині одно порожнин. гіперболоїда площиною XOZ і || до неї площинами: y=m. 3). Розглянемо перерізи одно порожнин. гіперболоїда площиною XOY і || до неї площинами. В перетині отримаємо:
Якщо h=0, то одерж., горловий еліпс: Якщо a=b, то отримаємо р-ня у вигляді: Всі асимптоти одно порожнин. гіперболоїда проходять через т.О і задовольняють р-ня: Двопорожнинним гіперболоїдом наз. поверхня, яка в деякій прямокут. с-мі коор.має р-ня: Оскільки змінні x,y,z входять в р-ня (25) тільки в парних степенях, то двопорожнин. гіперболоїд симетрич. відносно всіх коор. площин, осей і поч.. с-ми коор. Вісі OX і OY не перетин. двопорожнин. гіперболоїд. Вони наз. уявними, а вісь OZ перетин. його в точках Дослідимо форму двопорожнин. гіперболоїда методом перерізів і побуд. його. 1). Розглянемо перерізи двопорожнин. гіперболоїда площиною XOY і || до неї площинами:
Можливі три випадки: a). Якщо÷ h÷ < c то в перетині – порожня множина. b). Якщо÷ h÷ = c то отримаємо c). Якщо÷ h÷ > c то маємо еліпс, який збільшується з ростом ÷ h÷. 2). В площині YOZ і || до неї площинах отримаємо: 3). В площині XOZ і || до неї площинах маємо:
Якщо в р-ні (25) а=b, то поверхня наз. Двопорожнин.гіперболоїдом обертання. Його можна одержати обертанням гіперболи Еліптичним параболоїдом наз. поверхня, яка в деякі прямокутній с-мі коор.т має р-ня: Так як в р-ня (26) змінні x I y входять в парній степені, а z в непарній степені, то еліптичний параболоїдсиметричний відносно площин XOZ і YOZ та вісі OZ. Відносно інших координатних осей і площини XOY він не симетричний. Т.О(0,0,0) належить еліптичному параболоїду і наз. вершиною. Дослідимо форму еліптичного параболоїдаметодом перерізів і побуд. його.
1. Якщо h<0 – порожня множина. 2. Якщо h=0 – точка О(0,0,0). 3. Якщо h>0 – еліпс. 2). В площині YOZ і || до неї площинах отримаємо:
3). В площині XOZ і || до неї площинах отримаємо параболу (повністю аналогічно до попереднього) (рис.24). Якщо в р-ні (26) a=b, то отримаємо параболоїд обертання (навколо вісі OZ). Гіперболічним параболоїдом наз. поверхня, яка в деякі прямокутній с-мі коор. визначається р-ням: Так як в р-ня (27) змінні x I y входять в парній степені, а z в непарній степені, то гіперболічний параболоїдсиметрич. відносно площин XOZ і YOZ та вісі OZ. Відносно інших координат.х осей і площини XOY він не симетрич.. Т.О(0,0,0) належить гіперболічному параболоїду і наз. вершиною. Дослідимо форму гіперболічного параболоїдаметодом перерізів і побуд. його.
Можливі три випадки: a). Якщо h=0, то в перетині отрима. пару прямих, що перетин. в т.О(0,0,0). b). Якщо h>0, то отрим. гіперболу з віссю, яка || до вісі OX. c). Якщо h<0, то маємо гіперболу з віссю, яка || до вісі OY. 2). В площині YOZ і || до неї площинах отримаємо
3). В перетині гіперболічного параболоїда зплощиною XOZ і || до неї площинами також отрим. параболу з віссю || до вісі OZ (вітки направлені вверх):
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 559. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
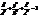 (22)
(22)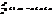 . Аналогічно для y і z:
. Аналогічно для y і z: 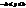 і
і 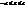 Отже, всі точки еліпсоїда лежать всередині прямокутного паралелепіпеда із сторонами 2а, 2b, 2с (крім вершин), з центром в точці О.
Отже, всі точки еліпсоїда лежать всередині прямокутного паралелепіпеда із сторонами 2а, 2b, 2с (крім вершин), з центром в точці О.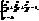 або
або 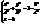 .
.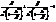 – еліпс. При зменшенні ú h÷ піввісі більшуються і коли h=0, одержуємо еліпс
– еліпс. При зменшенні ú h÷ піввісі більшуються і коли h=0, одержуємо еліпс 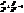 в площині XOY..
в площині XOY.. 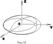
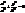 – дві уявні прямі, що перетинаються в дійсних точках С1(0,0,с); С2(0,0,-с).
– дві уявні прямі, що перетинаються в дійсних точках С1(0,0,с); С2(0,0,-с).
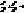 навколо осі OY. Такий еліпсоїд наз. еліпсоїдом обертання. Якщо ж в р-ні (22) а=b=с, то отримаємо сферу радіуса а.
навколо осі OY. Такий еліпсоїд наз. еліпсоїдом обертання. Якщо ж в р-ні (22) а=b=с, то отримаємо сферу радіуса а.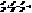 (24)
(24)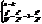 .
.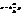 (з дійсною віссю, яка || до осі OY),
(з дійсною віссю, яка || до осі OY),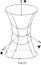
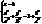 - еліпс.
- еліпс.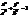 . При зростанні ÷ h÷ піввісі еліпса необмежено збільшуються разом із еліпсом. побудуємо горловий еліпс, та пару еліпсів в площинах паралельних до XOY (на однаковій відстані до неї) (рис.22).
. При зростанні ÷ h÷ піввісі еліпса необмежено збільшуються разом із еліпсом. побудуємо горловий еліпс, та пару еліпсів в площинах паралельних до XOY (на однаковій відстані до неї) (рис.22).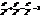 . Це одно порожнин. гіперболоїд обертання. Його можна отрим. обертанням гіперболи :
. Це одно порожнин. гіперболоїд обертання. Його можна отрим. обертанням гіперболи : 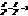 навколо вісі OZ.
навколо вісі OZ.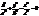 , тобто належать конусу, який наз. асимптотичним конусом однопорожнинного гіперболоїда.
, тобто належать конусу, який наз. асимптотичним конусом однопорожнинного гіперболоїда.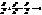 (25)
(25)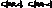 . які наз. вершинами. Вісь OZ наз. дійсною.
. які наз. вершинами. Вісь OZ наз. дійсною.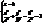 .
.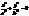 , тобто маємо точки
, тобто маємо точки 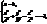 або
або 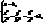 це гіпербола з віссю || до OZ. Побуд. її в площині YOZ (рис.23).
це гіпербола з віссю || до OZ. Побуд. її в площині YOZ (рис.23).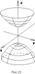
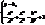 – гіпербола з віссю || до OZ. Побуд. її в площині XOZ (рис.23).
– гіпербола з віссю || до OZ. Побуд. її в площині XOZ (рис.23).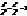 , яка знаходиться в площині XOZ навколо вісі OZ.
, яка знаходиться в площині XOZ навколо вісі OZ.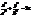 (26)
(26)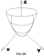 1). Розглянемо перерізи еліптичного параболоїдаплощиною XOY і || до неї площинами:
1). Розглянемо перерізи еліптичного параболоїдаплощиною XOY і || до неї площинами: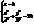 . Отримаємо:
. Отримаємо: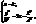 це парабола з віссю, яка || до вісі OZ (якщо k=0, то парабола з віссю OZ і з вершиною в точці О(0,0,0). Її і будуємо (рис.24)).
це парабола з віссю, яка || до вісі OZ (якщо k=0, то парабола з віссю OZ і з вершиною в точці О(0,0,0). Її і будуємо (рис.24)).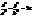 (27)
(27) 1). Розглянемо перерізи гіперболічного параболоїдаплощиною XOY і || до неї площинами:
1). Розглянемо перерізи гіперболічного параболоїдаплощиною XOY і || до неї площинами: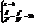 .
.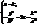 – параболу з віссю || до вісі OZ (вітки направлені вниз) (рис. 25).
– параболу з віссю || до вісі OZ (вітки направлені вниз) (рис. 25).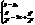 . (рис. 25)
. (рис. 25)